题目内容
1.(1)这三幅图中分别有多少个三角形呢?请填空.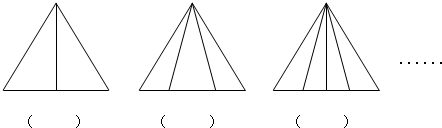
(2)如果照着这样画下去,第9幅图中一共有55个三角形.
(3)第n幅图中一共有$\frac{(n+1)(n+2)}{2}$个三角形.
分析 (1)此类问题的计数方法是:先数出图中的小三角形个数,如果图中有2个小三角形,那么图中的三角形总个数就是1+2=3;如果图中有3个小三角形,那么图中三角形的总个数就是1+2+3,此题图中一共有4个小三角形,那么图中的三角形个数就是:1+2+3+4,由此即可解答;
(2)根据上面的分析,第9个图形中是10个小三角形,所以一共有1+2+3+4+5+6+7+8+9+10个三角形;
(3)若是第n个图形,则有n+11个小三角形,所以一共有1+2+3+4+…+n-1+n+n+1个三角形,据此即可解答问题.
解答 解:(1)根据题干分析可得:1+2=3(个)
1+2+3=6(个)
1+2+3+4=10(个)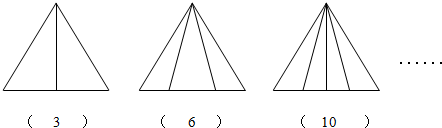
(2)1+2+3+4+5+6+7+8+9+10=55(个)
答:第9个图形一共有55个三角形.
(3)第n个图形一共有:
1+2+3+4+…+n-1+n+n+1
=$\frac{(n+1)(n+2)}{2}$(个)
答:第n个图形有$\frac{(n+1)(n+2)}{2}$个三角形.
故答案为:3;6;10;55;$\frac{(n+1)(n+2)}{2}$.
点评 此题主要考查了计数方法的应用,如果图形中的小三角形个数为n,则图中三角形的总个数就是1+2+3+…+n.

练习册系列答案
相关题目
11.
| 3千米=3000米 | 50000克=50千克 | 2平方米=200平方分米 |
| 900平方厘米=9平方分米 | 4元8角=4.8元 | 6分米=0.6米 |

