题目内容
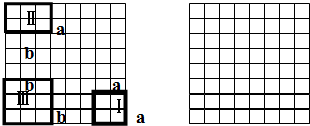
在8×8的正方形里有代号Ⅰ、Ⅱ、Ⅲ的矩形,要用若干块矩形(Ⅰ、Ⅱ、Ⅲ)在另一张8×8的正方形中拼出(2a+b)×(2b+a)的矩形怎么拼.用一张Ⅰ和一张Ⅱ拼出一个轴对称图形,能拼出几种拼几种,要求两个矩形至少有一条边在同一条直线上.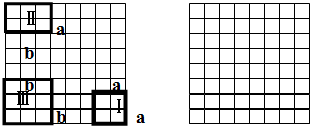

分析:(1)观察图形可知,若干把每个小方格的边长看做1,则拼组后的矩形的长和宽分别是2b+a=2×3+2=8;2a+b=2×2+3=7;据此利用图形Ⅰ、Ⅱ、Ⅲ的特点即可画出拼组后的图形;
(2)根据轴对称图形的定义:在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行作图.
(2)根据轴对称图形的定义:在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行作图.
解答:解:(1)根据题干分析可得:拼组后的矩形的长和宽分别是2b+a=2×3+2=8;2a+b=2×2+3=7;
据此利用图形Ⅰ、Ⅱ、Ⅲ的特点即可画出拼组后的图形如下所示:
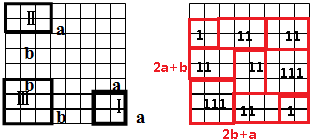
(2)根据轴对称图形的定义,利用图形Ⅰ、Ⅱ画出轴对称图形如下,一共有8种不同的拼组方法.

据此利用图形Ⅰ、Ⅱ、Ⅲ的特点即可画出拼组后的图形如下所示:

(2)根据轴对称图形的定义,利用图形Ⅰ、Ⅱ画出轴对称图形如下,一共有8种不同的拼组方法.

点评:本题考查了图形拼接前后图形面积不变即可求长方形形的长和宽;以及运用长方形形的对边相等这一性质即可画出拼接图,难度较大.

练习册系列答案
相关题目
 认一认,把图形的序号填在括号里.
认一认,把图形的序号填在括号里.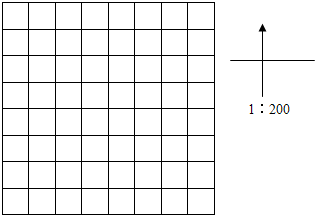 (2013?福田区模拟)学校有一块正方形草坪,如下8×8方格图,请你在草坪的东北角占正方形草坪的1/5范围里自由选定百分比给它涂色,使之构成一幅具有轴对称美的图案,这幅图案的面积占整个方格图面积的百分之几?如果按图案设计成花坛,根据图上的比例尺,算出你所设计花坛的实际周长(或面积).
(2013?福田区模拟)学校有一块正方形草坪,如下8×8方格图,请你在草坪的东北角占正方形草坪的1/5范围里自由选定百分比给它涂色,使之构成一幅具有轴对称美的图案,这幅图案的面积占整个方格图面积的百分之几?如果按图案设计成花坛,根据图上的比例尺,算出你所设计花坛的实际周长(或面积).