Question

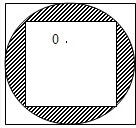如图所示，圆内有一个最大的正方形，已知正方形的面积为40平方厘米．求阴影部分的面积是

22.8

平方厘米．

Answer 1

分析：由图意可知：阴影部分的面积=圆的面积-正方形的面积，这个最大圆的直径应该等于正方形的对角线，据此即可用圆的半径表示出正方形的面积，正方形的面积已知，从而可以求出阴影部分的面积．

解答：解：如图，

设圆的半径为r，
则正方形的面积为：2r×r÷2×2=40，
即2r²=40，
   r²=20；
阴影部分的面积=3.14×20-40，
=62.8-40，
=22.8（平方厘米）；
答：阴影部分的面积是22.8平方厘米．
故答案为：22.8．

点评：解答此题的关键是用圆的半径表示出正方形的面积，再利用等量代换即可逐步求解．