题目内容
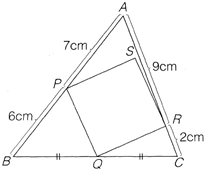 如图,正方形PQRS有三个顶点分别在三角形ABC的三条边上,BQ=QC,请求出正方形PQRS的面积.
如图,正方形PQRS有三个顶点分别在三角形ABC的三条边上,BQ=QC,请求出正方形PQRS的面积.分析:如下面左图所示,连接PR,根据题意可以表示出三角形APR,三角形BPQ,三角形CQR与三角形ABC的面积之间的关系,进而表示出三角形PQR的面积与三角形ABC的面积之间的关系,于是得出正方形PQRS的面积与三角形ABC的面积之间的关系,从而得出三角形ABC中除正方形之外的其余部分的面积与三角形ABC的面积之间的关系;然后再利用旋转的方式,如下面右图所示,将三角形BPQ以点P为中心逆时针旋转90°至三角形OPS,同样将三角形CQR以点R为中心,顺时针旋转90°至三角形ORS的位置,由BQ=CQ等关系可以得出图中两个阴影三角形恰好构成完整的四边形SPOR,连接AO,可以证明三角形APO,三角形ARO都是直角三角形,于是可以求出四边形APOR的面积,然后可以得出三角形ABC的面积,进而求出正方形PQRS的面积.
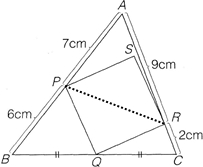
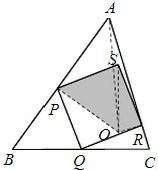


解答:解:如上面左图所示,连接PR,根据题意有:S△APR=S△ABC×
×
=
S△ABC,
S△BPQ=S△ABC×
×
=
S△ABC,
S△CQR=S△ABC×
×
=
S△ABC.
所以S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=(1-
-
-
)S△ABC=
S△ABC,
因此,S正方形PQRS=2S△PQR=
S△ABC,
S四边形APSR+S△BPQ+S△CQR=(1-
)S△ABC=
S△ABC;
如上面右图所示,将△BPQ以点P为中心逆时针旋转90°至△OPS,同样将△CQR以点R为中心,顺时针旋转90°至△ORS的位置,
因为BQ=CQ,∠PSO+∠RSO=∠PQB+∠RQC=90°,
所以两个阴影三角形可以构成完整的四边形SPOR.
连接AO,因为∠OPS+∠APS=∠BPQ+∠APS=90°,
所以△APO为直角三角形,同理△ARO也是直角三角形.
所以S四边形APSR+S△BPQ+S△CQR=S四边形APSR+S△OPS+S△OQS=S四边形APOR=S△APO+S△ARO=
×7×6+
×9×2=30(cm2),
因此S△ABC=30÷
=
,
S正方形PQRS=
×
=
=27.2(cm2).
答:正方形PQRS的面积是27.2cm2.
| 7 |
| 13 |
| 9 |
| 11 |
| 63 |
| 143 |
S△BPQ=S△ABC×
| 6 |
| 13 |
| 1 |
| 2 |
| 3 |
| 13 |
S△CQR=S△ABC×
| 2 |
| 11 |
| 1 |
| 2 |
| 1 |
| 11 |
所以S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=(1-
| 63 |
| 143 |
| 3 |
| 13 |
| 1 |
| 11 |
| 34 |
| 143 |
因此,S正方形PQRS=2S△PQR=
| 68 |
| 143 |
S四边形APSR+S△BPQ+S△CQR=(1-
| 68 |
| 143 |
| 75 |
| 143 |
如上面右图所示,将△BPQ以点P为中心逆时针旋转90°至△OPS,同样将△CQR以点R为中心,顺时针旋转90°至△ORS的位置,
因为BQ=CQ,∠PSO+∠RSO=∠PQB+∠RQC=90°,
所以两个阴影三角形可以构成完整的四边形SPOR.
连接AO,因为∠OPS+∠APS=∠BPQ+∠APS=90°,
所以△APO为直角三角形,同理△ARO也是直角三角形.
所以S四边形APSR+S△BPQ+S△CQR=S四边形APSR+S△OPS+S△OQS=S四边形APOR=S△APO+S△ARO=
| 1 |
| 2 |
| 1 |
| 2 |
因此S△ABC=30÷
| 75 |
| 143 |
| 2×143 |
| 5 |
S正方形PQRS=
| 2×143 |
| 5 |
| 68 |
| 143 |
| 136 |
| 5 |
答:正方形PQRS的面积是27.2cm2.
点评:本题难度很大,解决的关键是辅助线的添加,特别是通过旋转进行面积的转化.

练习册系列答案
相关题目
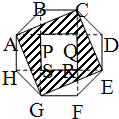 在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍?
在如图的正八边形ABCDEFGH中有两个正方形ACEG和PQRS.那么正八边形的面积是阴影部分面积的几倍? 如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积.
如图,ABCD是边长为5的正方形,E、F、G、H分别在边AB、BC、CD、DA上,且AE=BF=CG=DH=3,假定已知AF、BG、CH、DE围成的四边形PQRS是正方形,求图中阴影部分的面积. 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是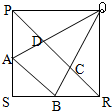 如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是________平方厘米.
如图,正方形PQRS的边长为12厘米,已知,AS=BS=4厘米,PA=BR=8厘米,则梯形ABCD的面积是________平方厘米.