题目内容
一个平行四边形和一个三角形的底相等,它们的面积的比是1:2,它们高的比是
- A.2:1
- B.1:4
- C.1:1
B
分析:平行四边形的面积=底×高,三角形的面积= ×底×高,再依据“它们的面积的比是1:2”,即可求出高之比.
×底×高,再依据“它们的面积的比是1:2”,即可求出高之比.
解答:设平行四边形的高为H,三角形的高为h,
平行四边形的面积:三角形的面积=1:2,
即2×底×H= 底×h,
底×h,
2H= h,
h,
所以H:h=1:4;
故答案为:B.
点评:解答此题的关键是依据题目条件表示出平行四边形和三角形的面积,进而求出它们的高之比.
分析:平行四边形的面积=底×高,三角形的面积=
 ×底×高,再依据“它们的面积的比是1:2”,即可求出高之比.
×底×高,再依据“它们的面积的比是1:2”,即可求出高之比.解答:设平行四边形的高为H,三角形的高为h,
平行四边形的面积:三角形的面积=1:2,
即2×底×H=
 底×h,
底×h,2H=
 h,
h,所以H:h=1:4;
故答案为:B.
点评:解答此题的关键是依据题目条件表示出平行四边形和三角形的面积,进而求出它们的高之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008?玉门市)作图:下面是一个等腰梯形,在梯形内画一条线段可以把它分成一个平行四边形和一个等腰三角形.请你画出这条线段.再从等腰三角形的顶点画出这个等腰三角形底边上的高.
(2008?玉门市)作图:下面是一个等腰梯形,在梯形内画一条线段可以把它分成一个平行四边形和一个等腰三角形.请你画出这条线段.再从等腰三角形的顶点画出这个等腰三角形底边上的高.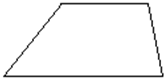
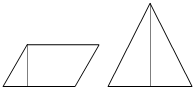 如图,一个平行四边形和一个三角形的面积相等,它们的底都是15厘米,平行四边形的高为6厘米,则三角形的高为
如图,一个平行四边形和一个三角形的面积相等,它们的底都是15厘米,平行四边形的高为6厘米,则三角形的高为