题目内容
【题目】如图所示,直角三角形ABC中,AB=5,BC=12,CA=13,PD、PE、PF分别垂直于边BC、CA、AB,其中D、E、F是垂足,已知PD=1,PE=2,则PF=

【答案】4.4
【解析】
试题分析:先连接PA、PB、PC,根据直角三角形ABC中,底AB=5,高BC=12,可求出三角形ABC的面积;根据三角形APC中底AC=13,高PE=2,可求出三角形APC的面积;根据三角形BPC中底BC=12,高PD=1,可求出三角形BPC的面积;再根据三角形ABC的面积﹣(三角形APC的面积+三角形BPC的面积)=三角形APB的面积,进而根据三角形APB的面积和底求得高PF的长度即可.
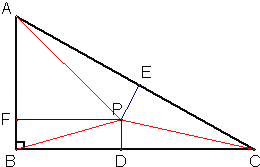
解:连接PA、PB、PC,由题意得:
三角形ABC的面积:![]() ×5×12=30,
×5×12=30,
三角形APC的面积:![]() ×13×2=13,
×13×2=13,
三角形BPC的面积:![]() ×12×1=6,
×12×1=6,
所以三角形APB的面积:30﹣(13+6)=30﹣19=11,
所以三角形APB的高:11![]() ÷5=22÷5=4.4;
÷5=22÷5=4.4;
故答案为:4.4.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
