题目内容
1.如图,已知四边形ABCD,AB垂直于BC,BC=7cm,AD垂直于DC,AD=3cm,∠BCD=45°,求四边形ABCD的面积.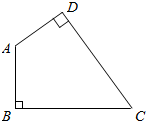
分析 延长BA、CD相交于点E,判断出△CBE是等腰直角三角形,再根据直角三角形两锐角的和是90°求出∠E=45°,然后判断出△ADE是等腰直角三角形,再求出DE,最后根据S四边形ABCD=S△CBE-S△ADE列式计算即可得解.
解答 解:如图,延长BA、CD相交于点E,
因为∠B=90°,∠BCE=45°,
所以△CBE是等腰直角三角形,
所以∠E=45°,BE=BC=7(厘米),
因为∠ADE=90°,∠E=45°,
所以△ADE是等腰直角三角形,
又因为AD=3厘米,
所以DE=3厘米,
因此S四边形ABCD=S△CBE-S△ADE
=7×7÷2-3×3÷2
=24.5-4.5
=20(平方厘米)
答:四边形ABCD的面积是20平方厘米.
点评 本题考查了等腰直角三角形的判定与性质,三角形的面积,作辅助线构造出等腰直角三角形是解题的关键.

练习册系列答案
相关题目
12.一堆煤12吨,每天用$\frac{1}{3}$吨,可用( )天.
| A. | 36 | B. | 4 | C. | 3 |
6.根据图形的变化规律,“?”处的图形应是( )

| A. |  | B. |  | ||
| C. |  |