Question

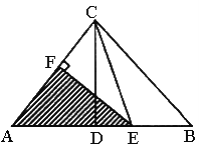
【题目】如图所示，2BE＝AE，CD和AE垂直，EF和AC垂直，△ABC的面积为60平方厘米，AC＝10厘米，CF＝6厘米，求△AEF的面积。________

Answer 1

【答案】16平方厘米

【解析】

根据三角形面积＝底×高÷2，高一定时，面积和底成正比例。由图可知：△ABC与△AEC共同一条高CD，2BE＝AE，进而可以求出△AEC的面积；同理△AEC与△AEF共同一条高EF，已知AC＝10厘米，CF＝6厘米，所以△AEF的底AF为10－6＝4（厘米），再通过三角形的面积即可求解。

△ABC与△AEC共同一条高CD，2BE＝AE，

所以△ABC面积∶△AEC面积＝AB∶AE＝（AE＋BE）∶AE＝3BE∶2BE＝3∶2。

解：设△AEC面积为X平方厘米。

△ABC面积∶△AEC面积＝3∶2＝60∶X

3X＝60×2

3X＝120

X＝120÷3

X＝40

同理△AEC与△AEF共同一条高EF，所以EF＝△AEC的面积÷AC×2＝40÷10×2＝8（厘米），

△AEF的面积＝AF×EF÷2＝（AC－CF）×EF÷2

＝（10－6）×8÷2

＝4×8÷2

＝32÷2

＝16（平方厘米）