题目内容
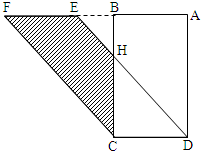 如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积.
如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积.
解:平行四边形的面积为:6×10=60(平方厘米),
三角形HCD的面积为:6×(10-4)÷2,
=6×6÷2,
=36÷2,
=18(平方厘米);
阴影部分的面积为:60-18=42(平方厘米);
答:阴影部分的面积是42平方厘米.
分析:由图意可知:长方形ABCD与平行四边形CDEF等底等高,则平行四边形的面积可求,阴影部分的面积=平行四边形的面积-空白三角形HCD的面积,代入数据即可求解.
点评:解答此题的关键是明白:长方形ABCD与平行四边形CDEF等底等高,从而容易求平行四边形的面积,进而求出阴影部分的面积.
三角形HCD的面积为:6×(10-4)÷2,
=6×6÷2,
=36÷2,
=18(平方厘米);
阴影部分的面积为:60-18=42(平方厘米);
答:阴影部分的面积是42平方厘米.
分析:由图意可知:长方形ABCD与平行四边形CDEF等底等高,则平行四边形的面积可求,阴影部分的面积=平行四边形的面积-空白三角形HCD的面积,代入数据即可求解.
点评:解答此题的关键是明白:长方形ABCD与平行四边形CDEF等底等高,从而容易求平行四边形的面积,进而求出阴影部分的面积.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是
如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是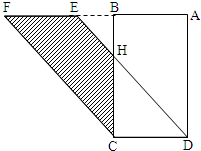 如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积.
如图,ABCD是长方形,AD长10厘米,AB长6厘米,CDEF是平行四边形,BH长4厘米,求图中阴影部分的面积. 如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是
如图,ABCD是个长方形,BCFE是个正方形,AB为10厘米,BC为4厘米,P为AD边上任意一点.图中阴影部分的面积是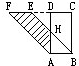 如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是________平方厘米.
如图,ABCD是长方形,长(AD)为8.4厘米,宽(AB)为5厘米,ABEF是平行四边形.如果DH长4厘米,那么图中阴影部分面积是________平方厘米.