题目内容
两个自然数之和是667,他们的最小公倍数除以最大公因数所得的商是120,且这两个数之差尽可能的大,则这两个数为________.
115,552
分析:首先假设这两数为a,b,由667=23×29,进行分析,如果23是它们的最大公约数的话,那么29就得拆成二个数的和,并且积是120,试验得到29=24+5,24×5=120,可得出两数;如果29是它们的最大公约数的话,那么23就得拆成二个数的和,并且积是120,试验得到23=15+8,15×8=120,从而得出两数.
解答:设这两数为a,b,最大公约数为d,最小公倍数为s,
则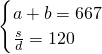 ,
,
最小公倍数除以最大公约数,所得的商是120.
①因为667=23×29,如果23是它们的最大公约数的话,那么29就得拆成二个数的和,
并且积是120,试验得到29=24+5,24×5=120;
故二数分别是24×23=552,5×23=115,
②如果29是它们的最大公约数的话,那么23就得拆成二个数的和,
并且积是120,试验得到23=15+8,15×8=120;
则二数分别是15×29=435,8×29=232.
因为这两个数之差尽可能的大,
所以a=115,b=552.
故答案为:115,552.
点评:此题主要考查了最大公约数与最小公倍数,由最小公倍数除以最大公约数所得商是120,进行分析是解决问题的关键.
分析:首先假设这两数为a,b,由667=23×29,进行分析,如果23是它们的最大公约数的话,那么29就得拆成二个数的和,并且积是120,试验得到29=24+5,24×5=120,可得出两数;如果29是它们的最大公约数的话,那么23就得拆成二个数的和,并且积是120,试验得到23=15+8,15×8=120,从而得出两数.
解答:设这两数为a,b,最大公约数为d,最小公倍数为s,
则
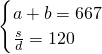 ,
,最小公倍数除以最大公约数,所得的商是120.
①因为667=23×29,如果23是它们的最大公约数的话,那么29就得拆成二个数的和,
并且积是120,试验得到29=24+5,24×5=120;
故二数分别是24×23=552,5×23=115,
②如果29是它们的最大公约数的话,那么23就得拆成二个数的和,
并且积是120,试验得到23=15+8,15×8=120;
则二数分别是15×29=435,8×29=232.
因为这两个数之差尽可能的大,
所以a=115,b=552.
故答案为:115,552.
点评:此题主要考查了最大公约数与最小公倍数,由最小公倍数除以最大公约数所得商是120,进行分析是解决问题的关键.

练习册系列答案
相关题目
 设上题答数是a,a的个位数字是b.七个圆内填入七个连续自然数,使每两个相邻圆内的数之和等于连线上的已知数,那么写A的圆内应填入
设上题答数是a,a的个位数字是b.七个圆内填入七个连续自然数,使每两个相邻圆内的数之和等于连线上的已知数,那么写A的圆内应填入