题目内容
(1)2001×20022002-2002×20012001
(2)2000-1+9×111×999
(3)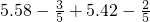
(4)2008-1+2-3+4-…+2006-2007.
解:(1)2001×20022002-2002×20012001,
=2001×2002×10001-2002×2001×10001,
=0;
(2)2000-1+9×111×999,
=1000+999+999×999,
=1000+999×(1+999),
=1000+999×1000,
=1000×(1+999),
=1000×1000,
=1000000;
(3)5.58- +5.42-
+5.42- ,
,
=5.58-0.6+5.42-0.4,
=5.58+5.42-(0.6+0.4),
=11-1,
=10;
(4)2008-1+2-3+4-…+2006-2007,
=-1+2-3+4+…-2005+2006-2007+2008,
=(2-1+)+(4-3)+…+(2006-2005)+(2008-2007),
=1×1004,
=1004.
分析:(1)把20022002看做2002×10001,把20012001看做2001×10001,从中发现,减号两边算式相同,故结果为1;
(2)2000-1=1000+999,9×111=999,运用乘法分配律简算;
(3)把分数化为小数,运用加法交换律与结合率以及减法的性质简算;
(4)原式可化为:-1+2-3+4+…-2005+2006-2007+2008,按次序每两个数分为一组,且和为1,2008个数中分为2008÷2=1004组,所以其和为1004.
点评:解答此题,应仔细观察算式,运用恰当的运算定律或性质进行简算.
=2001×2002×10001-2002×2001×10001,
=0;
(2)2000-1+9×111×999,
=1000+999+999×999,
=1000+999×(1+999),
=1000+999×1000,
=1000×(1+999),
=1000×1000,
=1000000;
(3)5.58-
 +5.42-
+5.42- ,
,=5.58-0.6+5.42-0.4,
=5.58+5.42-(0.6+0.4),
=11-1,
=10;
(4)2008-1+2-3+4-…+2006-2007,
=-1+2-3+4+…-2005+2006-2007+2008,
=(2-1+)+(4-3)+…+(2006-2005)+(2008-2007),
=1×1004,
=1004.
分析:(1)把20022002看做2002×10001,把20012001看做2001×10001,从中发现,减号两边算式相同,故结果为1;
(2)2000-1=1000+999,9×111=999,运用乘法分配律简算;
(3)把分数化为小数,运用加法交换律与结合率以及减法的性质简算;
(4)原式可化为:-1+2-3+4+…-2005+2006-2007+2008,按次序每两个数分为一组,且和为1,2008个数中分为2008÷2=1004组,所以其和为1004.
点评:解答此题,应仔细观察算式,运用恰当的运算定律或性质进行简算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用你喜欢的方法计算.
136×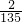 | 2001×3.14+200.1×31.4+20.01×314 |
 -[( -[( + + )× )×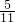 ] ] | 333×334+999×222 |
| 1.25×17.6+36.1÷0.8+2.63×12.5 |  ÷( ÷( +2.5× +2.5× ) ) |
 广州本田轿车2000--2004年产量销售情况统计表.
广州本田轿车2000--2004年产量销售情况统计表.