题目内容
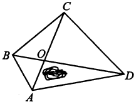 如图:某公园的外轮廓是四边形,被对角线AC、BD分成 四个部分,三角形AOD的面积是1平方千米,三角形BOC的面积是2平方千米,三角形COD的面积是3平方千米,公园陆地的面积是6平方千米,那么人工湖的面积是多少平方千米?
如图:某公园的外轮廓是四边形,被对角线AC、BD分成 四个部分,三角形AOD的面积是1平方千米,三角形BOC的面积是2平方千米,三角形COD的面积是3平方千米,公园陆地的面积是6平方千米,那么人工湖的面积是多少平方千米?分析:人工湖的面积是公园的总面积减去陆地面积,那么这里只要求出这个四边形的面积即可:
(1)因为三角形BOC的面积是2平方千米,三角形COD的面积是3平方千米,根据高一定时,三角形的面积与底成正比例的性质可得:BO:DO=2:3,
(2)再根据高一定时,三角形的面积与底成正比例的性质可得:三角形AOB的面积与三角形AOD的面积之比是2:3,由此即可求出三角形AOB的面积.
(1)因为三角形BOC的面积是2平方千米,三角形COD的面积是3平方千米,根据高一定时,三角形的面积与底成正比例的性质可得:BO:DO=2:3,
(2)再根据高一定时,三角形的面积与底成正比例的性质可得:三角形AOB的面积与三角形AOD的面积之比是2:3,由此即可求出三角形AOB的面积.
解答:解:因为三角形BOC的面积是2平方千米,三角形COD的面积是3平方千米,
所以可得:BO:DO=2:3,
则:三角形AOB的面积与三角形AOD的面积之比是2:3,因为三角形AOD的面积是1平方千米,
所以三角形AOB的面积是:1×2÷3=
(平方千米),
所以人工湖的面积是:1+2+3+
-6=
(平方千米),
答:人工湖的面积是
平方千米.
所以可得:BO:DO=2:3,
则:三角形AOB的面积与三角形AOD的面积之比是2:3,因为三角形AOD的面积是1平方千米,
所以三角形AOB的面积是:1×2÷3=
| 2 |
| 3 |
所以人工湖的面积是:1+2+3+
| 2 |
| 3 |
| 2 |
| 3 |
答:人工湖的面积是
| 2 |
| 3 |
点评:此题考查了高一定时,三角形的面积与高成正比例的性质的综合应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
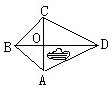 如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分.△AOB的面积是2平方千米,△COD的面积是3平方千米,公园陆地面积为6.92平方千米,那么人工湖的面积是
如图,某公园的外轮廓是四边形ABCD,被对角线AC、BD分成四个部分.△AOB的面积是2平方千米,△COD的面积是3平方千米,公园陆地面积为6.92平方千米,那么人工湖的面积是