题目内容
如图所示,直角三角形ABC的斜边AB长为10厘米,∠ABC=60°,此时BC长5厘米.以B点位中心,将△ABC顺时针旋转120°,点A、C分别到达点E、D的位置.求图中阴影部分的面积.
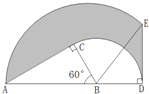

分析:由将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处,可得△ABC≌△EBD,由题给图象可知:S阴影=S扇形ABE+S△BDE-S△ABC-S扇形BCD=S扇形ABE-S扇形BCD可得出阴影部分面积.
解答:解:因为△ABC中,∠C是直角,AB=10cm,∠ABC=60°
所以AC=5
cm,BC=5cm
因为将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处
所以△ABC≌△EBD
由题给图象可知:
S阴影=S扇形ABE+S△BDE-S△ABC-S扇形BCD
=
+
×5×5
-
×5×5
-
=
=78.5(cm2)
答:AC边扫过的图形(阴影部分)的面积约是78.5cm2.
所以AC=5
| 3 |
因为将△ABC以点B为中心顺时针旋转,使点C旋转到AB的延长线上的点D处
所以△ABC≌△EBD
由题给图象可知:
S阴影=S扇形ABE+S△BDE-S△ABC-S扇形BCD
=
| 120π102 |
| 360 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 120π52 |
| 360 |
=
| 120π(102-52) |
| 360 |
=78.5(cm2)
答:AC边扫过的图形(阴影部分)的面积约是78.5cm2.
点评:本题考查了扇形面积的计算.

练习册系列答案
相关题目
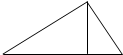 如图所示:直角三角形的三边长分别为6cm、8cm、10cm,则边长为10cm的边上的高为
如图所示:直角三角形的三边长分别为6cm、8cm、10cm,则边长为10cm的边上的高为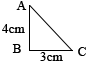 (2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个
(2008?高邮市)把如图所示的直角三角形ABC以BC为轴旋转一周,可以形成一个 请你在卡纸上画4个如图所示的直角三角形(单位:厘米)将它们剪下并拼成一个中间有一个小正方形空洞的大正方形.
请你在卡纸上画4个如图所示的直角三角形(单位:厘米)将它们剪下并拼成一个中间有一个小正方形空洞的大正方形.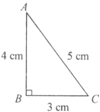 把如图所示的直角三角形ABC沿着AB轴旋转一周,形成
把如图所示的直角三角形ABC沿着AB轴旋转一周,形成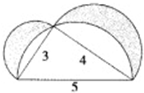 如图所示,直角三角形的直角边与斜边的长分别是3,4,5,以三边为直径分别作圆,则阴影部分的面积是
如图所示,直角三角形的直角边与斜边的长分别是3,4,5,以三边为直径分别作圆,则阴影部分的面积是