题目内容
16.一项工程,甲独做4天完成,乙独做5天完成,两队合做2天后,甲因事由乙接着完成,乙还要做0.5天才能完成任务.分析 将总工作量当作单位“1”,则甲每天完成全部的$\frac{1}{4}$,乙每天完成全部的$\frac{1}{5}$,两队合作每天可完成全部的$\frac{1}{4}$+$\frac{1}{5}$,根据乘法的意义,合作两天完成了全部的($\frac{1}{4}$+$\frac{1}{5}$)×2,根据分数减法的意义,此时还剩下全部的1-($\frac{1}{4}$+$\frac{1}{5}$)×2没有完成,根据分数除法的意义,用剩下工作量除以乙的工作效率,即得乙还要做几天才能完成任务.
解答 解:[1-($\frac{1}{4}$+$\frac{1}{5}$)×2]÷$\frac{1}{5}$
=[1-$\frac{9}{20}$×2]$÷\frac{1}{5}$
=[1-$\frac{9}{10}$]$÷\frac{1}{5}$
=$\frac{1}{10}$$÷\frac{1}{5}$
=0.5(天)
答:乙还要0.5天完成任务.
故答案为:0.5.
点评 首先根据已知条件求出剩下工作量,进而根据工作量÷工作效率=工作时间解答是完成本题的关键.

练习册系列答案
相关题目
6.把若干个1dm3的正方体拼成一个最小的正方体,这个正方体的体积是( )dm3.
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
11.在一个不透明的口袋里放入1个红球,2个黄球,3个绿球.(所放球除颜色不同,其他都相同)
(1)从口袋中任意摸出1个球,摸出绿球球的可能性最大,摸出红球球的可能性最小.
(2)小华从口袋中任意摸出1个球,摸后放回,一共摸了24次,摸出球的颜色情况记录如下:
根据上表中摸球的情况在表中用画“正”字的方法整理数据,再在图中用涂方格的方法记录红球、黄球和绿球摸出的次数.
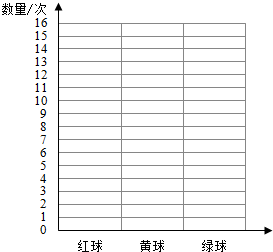
(1)从口袋中任意摸出1个球,摸出绿球球的可能性最大,摸出红球球的可能性最小.
(2)小华从口袋中任意摸出1个球,摸后放回,一共摸了24次,摸出球的颜色情况记录如下:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 颜色 | 绿 | 黄 | 绿 | 绿 | 红 | 黄 | 绿 | 绿 | 绿 | 黄 | 绿 | 绿 |
| 次数 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 颜色 | 红 | 绿 | 黄 | 红 | 绿 | 绿 | 黄 | 黄 | 绿 | 绿 | 绿 | 黄 |
| 颜 色 | 次 数 |
| 红球 | |
| 黄球 | |
| 绿球 |

1.甲数与乙数的比值是12,如果甲、乙两数都缩小$\frac{1}{10}$后,比值是( )
| A. | 1.2 | B. | 120 | C. | 12 | D. | 0.12 |
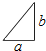 以b为轴旋转一周,得到的是一个圆锥,b是它的高,a是它的底面半径.
以b为轴旋转一周,得到的是一个圆锥,b是它的高,a是它的底面半径.