题目内容
2．有8个零件，其中7个质量相等，1个是次品，质量要重一些，用天平称，至少称几次能保证几次能找出这个零件来？分析 第一次：把8个零件分成3个，3个，2个三份，把其中两份3个零件的，分别放在天平秤两端，若天平秤平衡：则次品即在未取的2个零件中，再把2个零件分别放在天平秤两端，较低一端即为次品，若天平秤不平衡；第二次：把天平秤较低端的3个零件，任取2个，分别放在天平秤两端，若天平秤平衡，则未取零件即为次品，若不平衡，较低端的零件即为次品，据此即可解答．
解答 解：第一次：把8个零件分成3个，3个，2个三份，把其中两份3个零件的，分别放在天平秤两端，若天平秤平衡：则次品即在未取的2个零件中，再把2个零件分别放在天平秤两端，较低一端即为次品，若天平秤不平；
第二次：把天平秤较低端的3个零件，任取2个，分别放在天平秤两端，若天平秤平衡，则未取零件即为次品，若不平衡，较低端的零件即为次品．
点评 本题主要考查学生依据天平秤平衡原理解决问题的能力．
练习册系列答案
相关题目
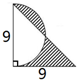面积：20.25平方厘米 
周长：21.98厘米．