题目内容
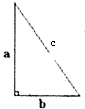如图，有一个直角三角形，它的两条直角边a、b的比是4：3．王华同学以直角边a为轴将三角形旋转得到了一个圆锥，李芳同学则以直角边b为轴将三角形旋转也得到了一个圆锥．你能求出王华同学和李芳同学所得到的两个圆锥的体积比是多少吗？
解：（
π32×4）：（π42×3）
=36：48，
=3：4；
答：王华同学和李芳同学所得到的两个圆锥的体积比是3：4．
分析：这个直角三角形的它的两条直角边a、b的比是4：3，可把直角边a看作4，b看作3．王华同学以直角边a为轴旋转得到的圆锥的高是4，底面半径是3，李芳同学以直角边b为轴得到的圆锥的高是3，底面半径是4，根据圆锥的体积公式V=πr2h即可求出王华同学和李芳同学所得到的两个圆锥的体积之比．
点评：本题主要是考查圆锥的意义及体积的计算、比的意义，关键是把这个直角三角形的两条直角边看作4和3，以不同的轴旋转得到的圆锥的高和底面积半径不同．
π32×4）：（π42×3）=36：48，
=3：4；
答：王华同学和李芳同学所得到的两个圆锥的体积比是3：4．
分析：这个直角三角形的它的两条直角边a、b的比是4：3，可把直角边a看作4，b看作3．王华同学以直角边a为轴旋转得到的圆锥的高是4，底面半径是3，李芳同学以直角边b为轴得到的圆锥的高是3，底面半径是4，根据圆锥的体积公式V=
πr2h即可求出王华同学和李芳同学所得到的两个圆锥的体积之比．点评：本题主要是考查圆锥的意义及体积的计算、比的意义，关键是把这个直角三角形的两条直角边看作4和3，以不同的轴旋转得到的圆锥的高和底面积半径不同．
练习册系列答案
相关题目
