题目内容
六(5)班分甲、乙两个小组游览东湖.已知甲组人数比乙组人数的
少3人.如果乙组中调1名同学到甲组,这时甲组的人数正好是乙组的
.求甲、乙两组原来的人数.[思路点击:设乙组原来有x人,则甲组原有(
x-3)人,列方程求解].
| 4 |
| 5 |
| 3 |
| 4 |
| 4 |
| 5 |
分析:设乙组原来有x人,根据题干“甲组人数比乙组人数的
少3人”可得甲组原有(
x-3)人,据此根据等量关系:甲组人数+1=(乙组人数-1)×
,列出方程解决问题.
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
解答:解:设乙组原来有x人,则甲组原有(
x-3)人,根据题意可得方程:
x-3+1=
(x-1)
x-2=
x-
x=
x=25
则甲组原有:25×
-3=17(人),
答:甲组原有17人,乙组原有25人.
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 4 |
| 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 20 |
| 5 |
| 4 |
x=25
则甲组原有:25×
| 4 |
| 5 |
答:甲组原有17人,乙组原有25人.
点评:此题属于含有两个未知数的应用题,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子来表示,进而列并解方程即可.

练习册系列答案
相关题目
 列式计算.
列式计算. 列式计算.
列式计算.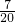 ,三天读完.这本书一共有多少页?
,三天读完.这本书一共有多少页? 还多4人,其中
还多4人,其中 的女生参加了花束队表演,参加表演的女生有多少人?
的女生参加了花束队表演,参加表演的女生有多少人?