题目内容
15．
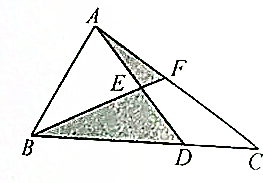△ABC的面积为1，AE=ED，BD=$\frac{2}{3}$BC，求阴影部分的面积．
分析 连接DF，根据已知和三角形面积公式得出S△ABE=S△DEF，S△BDF=2S△CDF，求出阴影部分的面积是S=S△BDF=S△ABF，即可得出S=$\frac{2}{5}$S△ABC，代入求出即可．
解答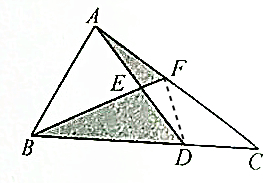 
解：连接DF，
因为AE=ED，BD=$\frac{2}{3}$BC，
所以S△ABE=S△BDE，S△AEF=S△DEF，S△BDF=2S△CDF，
所以阴影部分的面积S=S△BDF=S△ABF，
S=$\frac{2}{2+2+1}$S△ABC，
因为S△ABC=1，
所以S=1×$\frac{2}{5}$=$\frac{2}{5}$
答：阴影部分的面积是$\frac{2}{5}$．
点评 本题考查了三角形面积公式的应用，把阴影部分的面积转化是解答此题的关键，注意：等底等高的三角形的面积相等，等高的三角形的面积比等于对应底的比．
练习册系列答案
相关题目
圆柱形食品罐侧面的商标纸，展开后是边长为a cm的正方形（不计接口部分），这个食品罐的体积是$\frac{{a}^{3}}{4π}$cm3．