题目内容
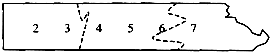 冬冬在一张纸条上依次写下2、3、4、5、6、7这6个数字,形成一个六位数.阿奇把这张纸条撕成了三节.这三节纸条上的数加起来得到的和(如图,三节纸条上的和为23+456+7=486)能被55整除.请问:阿奇可能是在什么位置撕断的这张纸条?
冬冬在一张纸条上依次写下2、3、4、5、6、7这6个数字,形成一个六位数.阿奇把这张纸条撕成了三节.这三节纸条上的数加起来得到的和(如图,三节纸条上的和为23+456+7=486)能被55整除.请问:阿奇可能是在什么位置撕断的这张纸条?考点:整除性质
专题:整除性问题
分析:由于2+3+4+5+6+7=27,所以分成的三段之和是9的倍数,又由于和能被55整除,所以和能被55×9=495整除,所以只要考虑撕成三节后的三个数相加的和是否为495的倍数即可.
解答:
解:因为2+3+4+5+6+7=27,
所以分成的三段之和是9的倍数,
又由于和能被55整除,
所以和能被55×9=495整除;
(1)假设撕成三节后的三个数相加的和是3位数,
则它们等于495或990,
①三个数的和最大是:2+34+567=603,所以不可能是990,
②因为23+456+7=486,所以不可能是495;
(2)根据①,可得撕成三节后的三个数相加的和是4位数,
①2+3+4567=4572,4572不是495的倍数,
②2+3456+7=3465,3465÷495=7,符合题意,
③2345+6+7=2358,2358不是495的倍数;
综上,可得阿奇是在2、3之间以及6、7之间撕断的这张纸条,得到的三个数分别是2、3456、7.
答:阿奇是在2、3之间以及6、7之间撕断的这张纸条,得到的三个数分别是2、3456、7.
所以分成的三段之和是9的倍数,
又由于和能被55整除,
所以和能被55×9=495整除;
(1)假设撕成三节后的三个数相加的和是3位数,
则它们等于495或990,
①三个数的和最大是:2+34+567=603,所以不可能是990,
②因为23+456+7=486,所以不可能是495;
(2)根据①,可得撕成三节后的三个数相加的和是4位数,
①2+3+4567=4572,4572不是495的倍数,
②2+3456+7=3465,3465÷495=7,符合题意,
③2345+6+7=2358,2358不是495的倍数;
综上,可得阿奇是在2、3之间以及6、7之间撕断的这张纸条,得到的三个数分别是2、3456、7.
答:阿奇是在2、3之间以及6、7之间撕断的这张纸条,得到的三个数分别是2、3456、7.
点评:解答此题的关键是分析出撕成三节后的三个数相加的和是495的倍数.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目

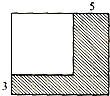 如图,把一个正方形的相邻两边分别增加3和5厘米,结果面积增加了71平方厘米(阴影部分).原正方形的面积为多少平方厘米?
如图,把一个正方形的相邻两边分别增加3和5厘米,结果面积增加了71平方厘米(阴影部分).原正方形的面积为多少平方厘米?