题目内容
甲、乙、丙三名工人共同做一批零件,甲加工了总数的 ,比乙少加工了24只,乙、丙加工零件数量的比是2:1.这批零件共有多少只?
,比乙少加工了24只,乙、丙加工零件数量的比是2:1.这批零件共有多少只?
解:乙加工零件总数的:
(1- )÷(1+2)×2,
)÷(1+2)×2,
=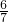 ÷(1+2)×2,
÷(1+2)×2,
=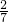 ×2,
×2,
= ;
;
这批零件共有:
24÷( -
- ),
),
=24÷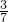 ,
,
=24× ,
,
=56(只);
答:这批零件共有56只.
分析:甲加工总数的 ,那么乙、丙共加工1-
,那么乙、丙共加工1- =
=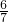 ,按比例分配,丙加工:
,按比例分配,丙加工: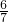 ÷(1+2)=
÷(1+2)=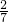 ,则乙加工
,则乙加工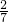 ×2=
×2= ,那么24只就占总数的
,那么24只就占总数的 -
- =
=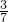 ,则零件总数为24÷
,则零件总数为24÷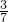 ,计算即可.
,计算即可.
点评:此题也可用方程解答:设甲加工的零件为x只,则零件总数为7x只,乙加工(x+24)只,丙加工(x+24)÷2只因此列出方程 x+(x+24)+(x+24)÷2=7x,解得x=8,所以一共有7x=56只零件.
(1-
 )÷(1+2)×2,
)÷(1+2)×2,=
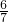 ÷(1+2)×2,
÷(1+2)×2,=
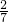 ×2,
×2,=
 ;
;这批零件共有:
24÷(
 -
- ),
),=24÷
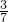 ,
,=24×
 ,
,=56(只);
答:这批零件共有56只.
分析:甲加工总数的
 ,那么乙、丙共加工1-
,那么乙、丙共加工1- =
=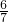 ,按比例分配,丙加工:
,按比例分配,丙加工: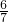 ÷(1+2)=
÷(1+2)=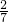 ,则乙加工
,则乙加工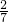 ×2=
×2= ,那么24只就占总数的
,那么24只就占总数的 -
- =
=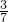 ,则零件总数为24÷
,则零件总数为24÷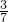 ,计算即可.
,计算即可.点评:此题也可用方程解答:设甲加工的零件为x只,则零件总数为7x只,乙加工(x+24)只,丙加工(x+24)÷2只因此列出方程 x+(x+24)+(x+24)÷2=7x,解得x=8,所以一共有7x=56只零件.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 ,比乙多加工了125只,乙丙加工数的比是3:2.这批零件共有多少只?
,比乙多加工了125只,乙丙加工数的比是3:2.这批零件共有多少只?