题目内容
6.求阴影部分的面积.
分析 连接OC,求阴影部分的面积,用$\frac{1}{3}$圆的面积减去减去三角形AOC的面积即可得到阴影部分的面积.
解答 解: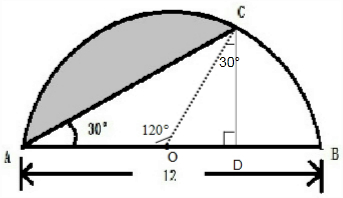
因为AB=12,OC=12÷2=6
在三角形OCD中,∠OCD=30°
所以OD=$\frac{1}{2}$OC=$\frac{1}{2}$×6=3,
所以CD2+OD2=OC2
CD2=36-9
即CD=3$\sqrt{3}$
所以三角形AOC的面积=6×3$\sqrt{3}$÷2=9$\sqrt{3}$.
阴影部分的面积:
3.14×(12÷2)2×$\frac{1}{3}$-9$\sqrt{3}$
=3.14×36×$\frac{1}{3}$-9$\sqrt{3}$
=37.68-9$\sqrt{3}$
答:阴影部分的面积37.68-9$\sqrt{3}$.
点评 本题运用圆的面积及三角形的面积公式进行解答即可.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
14.在长12.4cm,宽7.2cm的长方形中,剪半径是1cm的圆,能剪( )个.
| A. | 28 | B. | 29 | C. | 18 | D. | 17 |
18.如果把10米记作0米,11米记作+1,那么下面说法错误的是( )
| A. | 7米记作-7米 | B. | +8米表示实际18米 | ||
| C. | 4米记作-6米 |
16.直接写出得数.
| 287+399= | 16×0.25= | 6÷40%= | $\frac{5}{12}$÷$\frac{1}{6}$= |
| 3.14×202= | 48×($\frac{1}{6}$-$\frac{1}{8}$)= | 1-1÷5-$\frac{1}{5}$= | $\frac{1}{49}$:$\frac{1}{7}$=$\frac{1}{7}$. |