题目内容
18.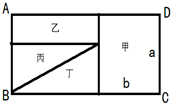 长方形ABCD被分成四个面积相等的甲、乙、丙、丁四部分,其中长方形甲的长与宽的比是a:b=3:2,求长方形乙长和宽的比?(请写出你的想法或计算过程)
长方形ABCD被分成四个面积相等的甲、乙、丙、丁四部分,其中长方形甲的长与宽的比是a:b=3:2,求长方形乙长和宽的比?(请写出你的想法或计算过程)
分析 a:b=3:2,设a是3,那么b就是2;长方形乙长是c,宽是d,那么乙的面积就是c×d,直角三角形丙的面积是:$\frac{1}{2}$×(a-d)×c,由乙和丙的面积相等,求出d的长度;再根据甲乙的面积相等求出c,然后作比即可.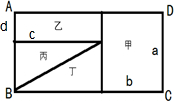
解答 解:设设a是3,那么b就是2;长方形乙长是c,宽是d;由乙和丙的面积相等可知:
c×d=$\frac{1}{2}$×(a-d)×c,
cd=$\frac{1}{2}$ac-$\frac{1}{2}$cd,
3cd=ac,
3d=a,
a=3,所以d=1;
由甲与乙的面积相等可知:
3×2=1×c,
c=6;
所以c:d=6:1.
答:长方形乙长和宽的比是6:1.
点评 本题抓住四个图形的面积相等这一条件,进行推算出长方形乙的长和宽,即可求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.46÷8=5…( )
| A. | 6 | B. | 7 | C. | 8 |