题目内容
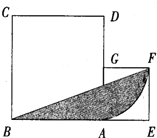图中是两个正方形，大正方形边长为8，小正方形边长为4，求图中阴影部分面积．
（单位：厘米），（π取3.14）
解：如图连接BG，AF，
因为三角形ABG与三角形AFB等底等高，所以三角形ABG的面积是：8×4÷2=16（平方厘米），
三角形AGF的面积是：4×4÷2=8（平方厘米），
扇形AGF的面积是：
×3.14×42，
=3.14×4，
=12.56（平方厘米），
阴影部分的面积：16+12.56-8=20.56（平方厘米），
答：阴影部分的面积是20.56平方厘米．
分析：连接BG，AF，则阴影部分的面积等于三角形ABG的面积+扇形AGF的面积-三角形AFG的面积，所以根据等底等高的三角形的面积相等，得出三角形ABG的面积等于三角形AFG的面积，进而根据三角形的面积公式与圆的面积公式解决问题．
点评：关键是将阴影部分的面积进行分割，再利用相应的公式分别求出各个部分的面积即可．
因为三角形ABG与三角形AFB等底等高，所以三角形ABG的面积是：8×4÷2=16（平方厘米），
三角形AGF的面积是：4×4÷2=8（平方厘米），
扇形AGF的面积是：
×3.14×42，=3.14×4，
=12.56（平方厘米），
阴影部分的面积：16+12.56-8=20.56（平方厘米），
答：阴影部分的面积是20.56平方厘米．
分析：连接BG，AF，则阴影部分的面积等于三角形ABG的面积+扇形AGF的面积-三角形AFG的面积，所以根据等底等高的三角形的面积相等，得出三角形ABG的面积等于三角形AFG的面积，进而根据三角形的面积公式与圆的面积公式解决问题．
点评：关键是将阴影部分的面积进行分割，再利用相应的公式分别求出各个部分的面积即可．
练习册系列答案
阅读快车系列答案
相关题目
图中有两个正方形，边长分别是6cm和4cm，图中最大的那个梯形的面积是
（2011?广州模拟）直角三角形的两直角边的长都是整厘米数，面积为59.5平方厘米．每次取四个同样的三角形围成（不重叠，不剪裁）含有两个正方形图案的图形（如图），在围成的所有正方形图案中，最小的正方形的面积是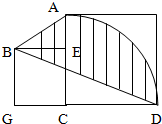
边长12厘米的大正方形 和边长10厘米的小正方形拼在一起，以两个正方形公有的顶点为圆心，以大正方形边长为半径事一条弧，再连接大，小正方形的两个顶点（如图），那么图中阴影总值的面积是
如图所示，在一个边长为1的大正方形中有两个小正方形，他们的面积分别为m、n．猜猜看，是m大还是n大？并求
图中有两个正方形，边长分别是6cm和4cm，图中最大的那个梯形的面积是________cm2．