题目内容
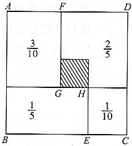一个正方形分成4个小长方形（如图），它们的面积分别为| 1 |
| 10 |
| 1 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
分析：大正方形的面积是：
+
+
+
=1（平方米）；大正方形的边长就是1米；
面积是
平方米的长方形和面积是
平方米的长方形的长相同，根据长方形的面积公式可知：它们的面积比是（FG×AF）：（FG×FD）=
：
，即：AF：FD=3：4；AF就是大正方形边长的
；同理：面积是
平方米的长方形的宽与面积是
平方米长方形的长相等，所以BE：EC=2：1，BE就是大正方形边长的
；
小正方形的边长GH=BE-AF，由此求出求出它的边长，进而求出面积．
| 3 |
| 10 |
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 10 |
面积是
| 3 |
| 10 |
| 2 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 3 |
| 7 |
| 1 |
| 5 |
| 1 |
| 10 |
| 2 |
| 3 |
小正方形的边长GH=BE-AF，由此求出求出它的边长，进而求出面积．
解答：解：
+
+
+
=1（平方米）；大正方形的边长就是1米；
（FG×AF）：（FG×FD）=
：
，那么：
AF：FD=3：4；
AF就是大正方形边长的
；
1×
=
（米）；
（BE×EF）：（EH×EC）=
：
；
BE：EC=2：1；
BE是大正方形边长的
；
1×
=
（米）；
GH=
-
=
（米）；
×
=
（平方米）；
答：阴影部分的面积是
平方米．
| 3 |
| 10 |
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 10 |
（FG×AF）：（FG×FD）=
| 3 |
| 10 |
| 2 |
| 5 |
AF：FD=3：4；
AF就是大正方形边长的
| 3 |
| 7 |
1×
| 3 |
| 7 |
| 3 |
| 7 |
（BE×EF）：（EH×EC）=
| 1 |
| 5 |
| 1 |
| 10 |
BE：EC=2：1；
BE是大正方形边长的
| 2 |
| 3 |
1×
| 2 |
| 3 |
| 2 |
| 3 |
GH=
| 2 |
| 3 |
| 3 |
| 7 |
| 5 |
| 21 |
| 5 |
| 21 |
| 5 |
| 21 |
| 25 |
| 441 |
答：阴影部分的面积是
| 25 |
| 441 |
点评：本题通过面积之间的比找出它们之间边长之间的关系，求出小正方形的边长，进而求出面积．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
有一正方形，通过多次划分，得到若干个正方形，具体操作如下：
第1次把它等分成4个小正方形，第2次将上次分成小正方形的其中一个又等分成4个小正方形，…，依此操作下去．
（1）通过观察和猜想，将第3次、第4次和第n次划分图中得到的正方形总个数（m）填入表中．
| 次数（n） | 第1次 | 第2次 | 第3次 | 第4次 | … | 第n次 |
| 正方形总个数（m） |