题目内容
一个直角梯形的周长是105厘米,两底之和与两腰之和的比是3:2,且其中一腰长是另一腰长的 ,这个直角梯形的面积是多少?
,这个直角梯形的面积是多少?
解:两底的和:105×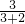 =63(厘米);
=63(厘米);
两腰的和:105-63=42(厘米);
较短的腰:42× =12(厘米);
=12(厘米);
梯形的面积:63×12÷2,
=756÷2,
=378(平方厘米);
答:这个直角梯形的面积是378平方厘米.
分析:这个梯形的周长已知,再据“两底之和与两腰之和的比是3:2”即可分别求出两底的和与两腰的和;又因“且其中一腰长是另一腰长的 ”,则较短的腰占两腰和的
”,则较短的腰占两腰和的 ,且较短的腰就是梯形的高,于是利用梯形的面积公式即可求解.
,且较短的腰就是梯形的高,于是利用梯形的面积公式即可求解.
点评:解答此题的关键是先求出两底的和与两腰的和,进而求出较短的腰,且要明白较短的腰就是梯形的高,从而问题得解.
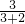 =63(厘米);
=63(厘米);两腰的和:105-63=42(厘米);
较短的腰:42×
 =12(厘米);
=12(厘米);梯形的面积:63×12÷2,
=756÷2,
=378(平方厘米);
答:这个直角梯形的面积是378平方厘米.
分析:这个梯形的周长已知,再据“两底之和与两腰之和的比是3:2”即可分别求出两底的和与两腰的和;又因“且其中一腰长是另一腰长的
 ”,则较短的腰占两腰和的
”,则较短的腰占两腰和的 ,且较短的腰就是梯形的高,于是利用梯形的面积公式即可求解.
,且较短的腰就是梯形的高,于是利用梯形的面积公式即可求解.点评:解答此题的关键是先求出两底的和与两腰的和,进而求出较短的腰,且要明白较短的腰就是梯形的高,从而问题得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目