题目内容
【题目】用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。图①②③④中,三面、两面、一面涂色及没有涂色的小正方体各有多少块?
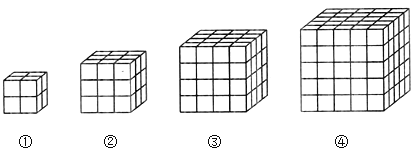
(1)完成下表。
三面涂色 的块数 | 两面涂色 的块数 | 一面涂色 的块数 | 没有涂色 的块数 | |
① | ||||
② | ||||
③ | ||||
④ |
(2)先观察上边,再填空。
如果一个大的正方体每条棱上有n块(n≥3)小正方体,则:
①三面涂色的小正方体位于顶点处,每个顶点上有一块,共有( )块。
②两面涂色的小正方体位于棱长上,每条棱长上有( )块,共有( )块。
③一面涂色的小正方体位于面上,每个面中间有( )块,共有( )块。
④没有涂色的小正方体位于大正方体的内部,共有( )块。
(3)你能写出第⑨个大正方体中4类小正方体的块数吗?
【答案】(1)①8 0 0 0 ②8 12 6 1 ③8 24 24 8 ④8 36 54 27
(2)①8 ②n-2 12(n-2) ③(n-2)2 6(n-2)2 ④(n-2)3
(3)8 96 384 512
【解析】
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下面的图形中哪些是直线?哪些是射线?哪些是线段?它们有什么区别和联系?(按序号的先后顺序来填写)
|
|
|
|
1 | 2 | 3 | 4 |
|
|
| |
5 | 6 | 7 |
直线:________
射线:________、________、________
线段:________、________