题目内容
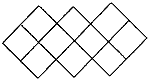 10个连续的自然数,上题的答数是其中第三大的数.把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等.那么,这个和数最小是
10个连续的自然数,上题的答数是其中第三大的数.把这10个数填到下图的方格中,每格填一个数,要求图中三个2×2的正方形中四数之和相等.那么,这个和数最小是24
24
.分析:10个连续自然数中,9是其中第三大的数,所以这10个自然数为2,3,4,5,6,7,8,9,10,11.图中三个2×2的正方形中四数之和相等,所以2+3+…+11再加上两个重复的数,和被3整除;因为2+3+…+11=65,要使和数最小,两个重复数的和应最小,这两个数可以取2与5,或3与4.这时和数是24.据此解答.
解答:解:10个连续自然数中,9是其中第三大的数,所以这10个自然数为2,3,4,5,6,7,8,9,10,11.
图中三个2×2的正方形中四数之和相等,所以2+3+…+11再加上两个重复的数,和被3整除
因为2+3+…+11=65,
要使和数最小,两个重复数的和应最小,这两个数可以取2与5,或3与4.这时和数是24.和数为24是可能的,
如以下两图:
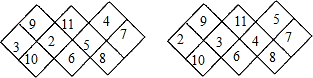
故答案为:24.
图中三个2×2的正方形中四数之和相等,所以2+3+…+11再加上两个重复的数,和被3整除
因为2+3+…+11=65,
要使和数最小,两个重复数的和应最小,这两个数可以取2与5,或3与4.这时和数是24.和数为24是可能的,
如以下两图:

故答案为:24.
点评:关键是明确9是其中第三大的数,所以这10个自然数为2,3,4,5,6,7,8,9,10,11.

练习册系列答案
相关题目
