题目内容
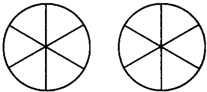用A、B、C、D、E、F六种燃料去染下图的两个调色盘，要求每个调色盘里的六种颜色不能相同，且相邻四种颜色在两个调色盘里不能重复，那么共有488160
488160
种不同的染色方案（旋转算不同方法）．分析：由于有两个调色盘，先在两个调色盘中选一个，则在这个调色盘里有6×5×4×3×2×1=720种染法，再看另外一个调色盘，相邻的四种颜色重复分为4个重复，5个重复和6个重复，但由于5个重复6个就必然重复，所以只要分4和6两种就行了．4种颜色重复有6种情况，6种颜色重复只有1种．每种情况经旋转可变出6种．所以共有6×5×4×3×2×1-1×6-6×6=678．总共有678×720=488160种．
解答：解：在一个调色盘里有有6×5×4×3×2×1=720种染法；
再看另外一个调色盘，相邻的四种颜色重复分为4个重复，5个重复和6个重复，
由于5个重复6个就必然重复，所以只要分4和6两种就行了．
4种颜色重复有6种情况，6种颜色重复只有1种，每种情况经旋转可变出6种；
所以共有6×5×4×3×2×1-1×6-6×6=678，
所以总共有678×720=488160种．
故答案为：488160．
再看另外一个调色盘，相邻的四种颜色重复分为4个重复，5个重复和6个重复，
由于5个重复6个就必然重复，所以只要分4和6两种就行了．
4种颜色重复有6种情况，6种颜色重复只有1种，每种情况经旋转可变出6种；
所以共有6×5×4×3×2×1-1×6-6×6=678，
所以总共有678×720=488160种．
故答案为：488160．
点评：完成本题要在了解简单的排列组合知识的基础上完成．
练习册系列答案
相关题目
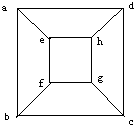如图8个顶点分别用a，b，c，d，e，f，g，h表示．每个顶点上的数是与它相邻三个顶点数和的