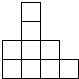题目内容
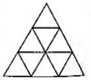 如图是一个由9个相同的小等边三角形所组成的大等边三角形.现在要把一枚黑子和一枚白子分别被放入两个小等边三角形中,并且要求这两个小等边三角形既没有公共边也没有公共顶点,那么共有
如图是一个由9个相同的小等边三角形所组成的大等边三角形.现在要把一枚黑子和一枚白子分别被放入两个小等边三角形中,并且要求这两个小等边三角形既没有公共边也没有公共顶点,那么共有24
24
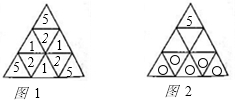
种不同的放置方法.分析:此题采用枚举法解答.枚举黑子的放置情况,当把黑子依次放在小等边三角形中,可把放置相应的白子的方法数写在小等边三角形内(如图1).例如“5”表示把黑子放在这一格时,相应的白子由5种放法(如图2),一共有(5+2+1)×3=24种不同的放置方法.
解答:解:
不同的放置方法一共有:
(5+2+1)×3=24(种).
答:共有24种不同的放置方法.
故答案为:24.

不同的放置方法一共有:
(5+2+1)×3=24(种).
答:共有24种不同的放置方法.
故答案为:24.
点评:此题考查了学生用枚举的方法解答问题的能力,以及对对称性的认识.图形的特殊性决定了本题很难直接用乘法原理解决.此题还有一个难点在于“要求这两个小等边三角形既没有公共边也没有公共顶点”,这个条件容易遗漏,因此会出现多算或漏算的情况.

练习册系列答案
相关题目

 (2012?建华区)如图是一个由9个相同的小正方体组成的立体图形,从前面看到形状应该是( ),从上面看到的形状应该是( )
(2012?建华区)如图是一个由9个相同的小正方体组成的立体图形,从前面看到形状应该是( ),从上面看到的形状应该是( )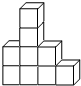 如图是一个由9个相同的小正方体组成的立体图形,从前面看到形状应该是______,从上面看到的形状应该是______
如图是一个由9个相同的小正方体组成的立体图形,从前面看到形状应该是______,从上面看到的形状应该是______