题目内容
【题目】如下图的6条线分别连接着九个○,其中一个○里的数字是6.请你选九个连续自然数(包括6在内),填入○内,使每条线上各数的和都等于23.

【答案】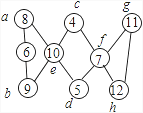
【解析】
当六条线上的数分别相加时,数6只加了1次,其余各数分别加了两次.又已知每条对角线上各数之和都等于23,所以这九个连续自然数之和应是(6×23+6)÷2=72.
于是九个数的中间数是72÷9=8,由此可知这九个连续自然数是4,5,6,7,8,9,10,11,12.其中显然只有11+12=23,故x=11,y=12和x=12,y=11.
首先考虑x=11,y=12的情况.注意7若不与x或y在一条线上,则23﹣7=16,只能表示成10+6,而过7的线段却有两条,所以必须f=7,于是c=4,d=5,再由a+b=23﹣6=17,可知a、b均不为10,e=10,a=8,b=9,于是得到下图:
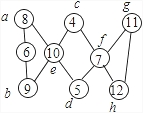
当x=12,y=11时,同理可得:f=7,g=11,h=12.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
