题目内容
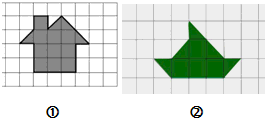 阴影部分的面积是多少?(每个小方格的面积表示1cm2)
阴影部分的面积是多少?(每个小方格的面积表示1cm2)
图①的阴影部分面积是________,
图②的阴影部分面积是________.
12cm2 6.5cm2
分析:(1)把两边的三角形拼接到右上角就成为了一个长为3厘米,宽为4厘米的长方形,那么长方形的面积就是图①的阴影部分面积;
(2)同理,把上边和左边的三角形拼接到中间梯形的左右两边,就成为了一个长为3厘米,宽为2厘米的长方形,和一个直角边都是1厘米的三角形,那么这两部分的面积和就是图②的阴影部分的面积.
解答:根据分析可得:
图①的阴影部分面积:3×4=12(平方厘米);
图②的阴影部分面积:3×2+1×1÷2=6+0.5=6.5(平方厘米);
答:图①的阴影部分面积是12cm2,图②的阴影部分面积是6.5cm2.
故答案为:12cm2,6.5cm2.
点评:本题要利用“割补法”进行等积变形,这样计算起来会更简单;考查的知识点:三角形的面积公式:S=ah÷2;长方形的面积公式:S=ab.
分析:(1)把两边的三角形拼接到右上角就成为了一个长为3厘米,宽为4厘米的长方形,那么长方形的面积就是图①的阴影部分面积;
(2)同理,把上边和左边的三角形拼接到中间梯形的左右两边,就成为了一个长为3厘米,宽为2厘米的长方形,和一个直角边都是1厘米的三角形,那么这两部分的面积和就是图②的阴影部分的面积.
解答:根据分析可得:
图①的阴影部分面积:3×4=12(平方厘米);
图②的阴影部分面积:3×2+1×1÷2=6+0.5=6.5(平方厘米);
答:图①的阴影部分面积是12cm2,图②的阴影部分面积是6.5cm2.
故答案为:12cm2,6.5cm2.
点评:本题要利用“割补法”进行等积变形,这样计算起来会更简单;考查的知识点:三角形的面积公式:S=ah÷2;长方形的面积公式:S=ab.

练习册系列答案
相关题目
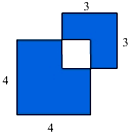 如图,边长分别是4厘米、3厘米的大小两个正方形的重合部分面积是2平方厘米,阴影部分的面积是多少平方厘米?.
如图,边长分别是4厘米、3厘米的大小两个正方形的重合部分面积是2平方厘米,阴影部分的面积是多少平方厘米?. 厘米?
厘米?