题目内容
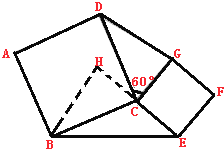
【题目】如图,已知边长为5的正方形ABCD和边长为3的正方形CEFG共顶点C,正方形CEFG绕点C旋转60°,连接BE、DG,则△BCE的面积与△CDG的面积比是 .

【答案】1:1
【解析】
试题分析:(1)在△BCE中根据正弦定理,它的面积是![]() ,BC是边长为5的正方形ABCD的边长,所以BC=5,CE是边长为3的正方形CEFG的边长,所以CE=3,正方形CEFG绕点C旋转60°,可求出∠BCE=120°,可求出△BCE的面积;同理在△CDG中根据正弦定理求出它的面积.据此可解答.
,BC是边长为5的正方形ABCD的边长,所以BC=5,CE是边长为3的正方形CEFG的边长,所以CE=3,正方形CEFG绕点C旋转60°,可求出∠BCE=120°,可求出△BCE的面积;同理在△CDG中根据正弦定理求出它的面积.据此可解答.
(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.
解:(1)S△BCE=![]() =
=![]() ;
;
S△CDG=![]() =
=![]() ;
;
因sin120°=sin60°
S△BCE:S△CDG=(![]() ):(
):(![]() )=1:1;
)=1:1;
故答案为;1:1.
(2)(2)将△CDG逆时针旋转90°,得到△CBH,H、C、E共线,△CDG与△CBH的高相等,又因CH=CE=3,根据三角形的面积公式可求出它们的比.
S△CDG=S△CBH=![]() ,
,
S△BCE=![]() ,
,
S△BCE:S△CDG=(![]() ):(
):(![]() )=1:1,
)=1:1,
故答案为;1:1.

练习册系列答案
相关题目
【题目】下面是李明和张强两名同学跳远比赛成绩的统计表。
姓名成绩/米次数 | 一 | 二 | 三 |
李明 | 4.3 | 4.8 | 4.1 |
张强 | 4.0 | 2.7 | 5.0 |
(1)根据统计表中的数据,完成下面的折线统计图。

(2)两名同学跳远的最好成绩分别是多少?
(3)张强第几次的成绩超过了李明?
(4)从统计图中,你还知道了什么?


