题目内容
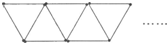 如图,用火柴棒组成三角形图案.如是在图案中共用了2005根火柴棒,那么图案中共有________个三角形.
如图,用火柴棒组成三角形图案.如是在图案中共用了2005根火柴棒,那么图案中共有________个三角形.
1002
分析:搭一个三角形需3根火柴,搭2个三角形中间少用1根,需要5根火柴棒,搭3个三角形中间少用2根,需要7根火柴棒,搭4个三角形中间少用3根,需要9根火柴棒…搭n个三角形中间少用(n-1)根,需要[3n-(n-1)]=2n+1根火柴棒,由此即可求得2005根小棒组成的三角形个数.
解答:设2005根小棒共组成了n个三角形,根据题干分析可得:
2n+1=2005,
2n=2004,
n=1002,
答:图案中共有1002个三角形.
点评:此题主要考查了图形的变化类,注意结合图形,发现蕴含的规律,找出解决问题的途径,此题也可以直接列式:(2005-1)÷2=1002(个)
分析:搭一个三角形需3根火柴,搭2个三角形中间少用1根,需要5根火柴棒,搭3个三角形中间少用2根,需要7根火柴棒,搭4个三角形中间少用3根,需要9根火柴棒…搭n个三角形中间少用(n-1)根,需要[3n-(n-1)]=2n+1根火柴棒,由此即可求得2005根小棒组成的三角形个数.
解答:设2005根小棒共组成了n个三角形,根据题干分析可得:
2n+1=2005,
2n=2004,
n=1002,
答:图案中共有1002个三角形.
点评:此题主要考查了图形的变化类,注意结合图形,发现蕴含的规律,找出解决问题的途径,此题也可以直接列式:(2005-1)÷2=1002(个)

练习册系列答案
相关题目
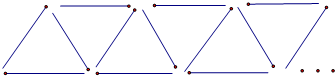 如图,它是由火柴棒组成的三角形图案,如果在这个三角形图案中,用了2001根火柴,那么它共有三角形
如图,它是由火柴棒组成的三角形图案,如果在这个三角形图案中,用了2001根火柴,那么它共有三角形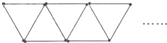 如图,用火柴棒组成三角形图案.如是在图案中共用了2005根火柴棒,那么图案中共有
如图,用火柴棒组成三角形图案.如是在图案中共用了2005根火柴棒,那么图案中共有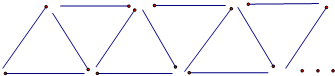 如图,它是由火柴棒组成的三角形图案,如果在这个三角形图案中,用了2001根火柴,那么它共有三角形________个.
如图,它是由火柴棒组成的三角形图案,如果在这个三角形图案中,用了2001根火柴,那么它共有三角形________个.