题目内容
16.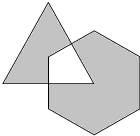 如图所示,正三角形的一个顶点在正六边形的中心,且正六边形的面积是3cm2,正三角形的面积是2cm2,求阴影部分的面积.
如图所示,正三角形的一个顶点在正六边形的中心,且正六边形的面积是3cm2,正三角形的面积是2cm2,求阴影部分的面积.
分析 如图,根据正六边形的中心到各顶点的距离相等可得CI=CD,再根据∠2+∠3=∠1+∠2=60°,可以证明∠1=∠3,然后即可证明△CDN与△CIN全等,从而得到重叠部分的面积等于以正六边形的边长为边的等边三角形的面积,即正六边形面积的$\frac{1}{6}$,进而解决问题.
解答 解:根据正六边形和正三角形的性质,可知CI=CD,
因为∠2+∠3=∠1+∠2=60°,所以∠1=∠3,
在△CIN和△CDM中,∠MDC=∠NIC=60°,CI=CD,∠1=∠3,
所以△CIM≌△CDM,
所以S△CIN=S△CDM,
所以重叠部分的面积是正六边形的$\frac{1}{6}$,即3×$\frac{1}{6}$=0.5(平方厘米)
所以阴影部分的面积为:
(2-0.5)+(3-0.5)
=1.5+2.5
=4(平方厘米)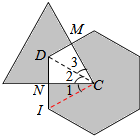
答:阴影部分的面积为4平方厘米.
点评 此题解答的关键在于求出正六边形的$\frac{1}{6}$的面积.进而得出空白部分的面积,解决问题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.一个数的( )的个数是无限的.
| A. | 因数 | B. | 倍数 | C. | 素数 |