题目内容
如图,一只装了水的密封瓶子,其内部可以看成是由底面是边长分别为2cm和6cm的两个长方体组成的简单几何体.两种放置方式液体的高度不同,则这个简单几何体的总高度是多少?
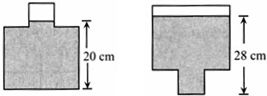
解:设几何体的高为h厘米,两次放置没有水的部分体积相等,
得:(h-20)×22=(h-28)×62,
4h-80=36h-1008,
32h=928,
h=29;
答:这个简单几何体的总高度是29厘米.
分析:设出几何体的高,利用没有水的体积相等,列出方程解答即可得到结果.
点评:几何体的表面积、体积的运算不是单纯的表面积或体积公式的直接运用,往往与三视图或与推理知识相结合.
得:(h-20)×22=(h-28)×62,
4h-80=36h-1008,
32h=928,
h=29;
答:这个简单几何体的总高度是29厘米.
分析:设出几何体的高,利用没有水的体积相等,列出方程解答即可得到结果.
点评:几何体的表面积、体积的运算不是单纯的表面积或体积公式的直接运用,往往与三视图或与推理知识相结合.

练习册系列答案
相关题目
直接写出下面各题的得数.
| 34×5= | 0.37+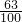 = = | 0.99÷1.l= | 10.6-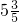 = = |
 × × = = | 0.375÷ = = | 40×101= | 254+98= |

