题目内容
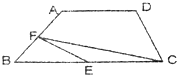 如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.
如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.若三角形EFC的面积为a,则梯形ABCD的面积是
分析:如图,连接AE,因为BC=2AD,E为BC的中点,所以四边形AECD是平行四边形,且三角形ABE和平行四边形AECD等底等高,所以平行四边形的面积是这个三角形的面积的2倍,又因为三角形EFC的面积为a,所以三角形BEF的面积也是a,又因为F是AB的中点,所以可得三角形ABE的面积是2a,则平行四边形的面积就是2a×2=4a,据此即可解答问题.


解答:解:连接AE,因为BC=2AD,E为BC的中点,所以四边形AECD是平行四边形,
且三角形ABE和平行四边形AECD等底等高,所以平行四边形的面积是这个三角形的面积的2倍,
又因为三角形EFC的面积为a,所以三角形BEF的面积也是a,
又因为F是AB的中点,所以可得三角形ABE的面积是2a,
则平行四边形的面积就是2a×2=4a,
所以这个梯形的面积是2a+4a=6a.
答:则梯形ABCD的面积是 6a.
故答案为:6a.
且三角形ABE和平行四边形AECD等底等高,所以平行四边形的面积是这个三角形的面积的2倍,
又因为三角形EFC的面积为a,所以三角形BEF的面积也是a,
又因为F是AB的中点,所以可得三角形ABE的面积是2a,
则平行四边形的面积就是2a×2=4a,
所以这个梯形的面积是2a+4a=6a.
答:则梯形ABCD的面积是 6a.
故答案为:6a.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质以及等底等高的平行四边形是三角形的面积的2倍的灵活应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (2012?北京)如图:梯形ABCD中,AD∥BC,AC、BD交于M,
(2012?北京)如图:梯形ABCD中,AD∥BC,AC、BD交于M,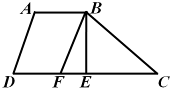 如图,梯形ABCD中,上底AB的长度是10厘米,梯形的高BE的长度是12厘米,且E是CD中点,BF将梯形ABCD分成面积相等的两部分.那么,EF的长度是
如图,梯形ABCD中,上底AB的长度是10厘米,梯形的高BE的长度是12厘米,且E是CD中点,BF将梯形ABCD分成面积相等的两部分.那么,EF的长度是 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?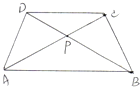 如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有
如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有