题目内容
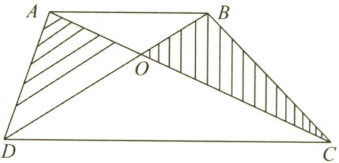 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?分析:由图意可知:三角形ADC和三角形BDC等底等高,则二者的面积相等,分别减去公共部分(三角形DOC),则剩余的部分面积也相等,即两个阴影三角形的面积相等,于是即可求出它们二者各自的面积;进而可以得出AO:OC=1:3(等底不等高的三角形的面积比就等于其对应底的比),则三角形AOB和三角形BOC的面积比也是1:3,从而可以求出三角形AOB的面积,梯形的面积就等于四个三角形的面积和,据此解答即可.
解答:解:据分析解答如下:
S△ADO=S△BOC=12÷2=6(平方厘米),
AO:OC=6:18=1:3,
S△AOB:S△BOC=1:3,
S△AOB=6÷3=2(平方厘米),
所以S梯形ABCD=2+12+18=32(平方厘米);
答:梯形ABCD的面积是32平方厘米.
S△ADO=S△BOC=12÷2=6(平方厘米),
AO:OC=6:18=1:3,
S△AOB:S△BOC=1:3,
S△AOB=6÷3=2(平方厘米),
所以S梯形ABCD=2+12+18=32(平方厘米);
答:梯形ABCD的面积是32平方厘米.
点评:解答此题的主要依据是:等底不等高的三角形的面积比就等于其对应底的比.

练习册系列答案
相关题目
 如图在梯形 ABCD中,甲三角形的面积大于乙三角形的面积
如图在梯形 ABCD中,甲三角形的面积大于乙三角形的面积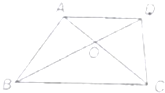 如图在梯形ABCD中,两条对角线AC、BD相交于O点,已知AO=
如图在梯形ABCD中,两条对角线AC、BD相交于O点,已知AO=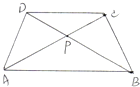 如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有
如图在梯形ABCD 中,AB平行于CD,AC与BD 相交于点P,则图中面积相等的三角形共有 如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?
如图在梯形ABCD中,AB和CD分别为梯形的上底和下底,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是多少平方厘米?