题目内容
看图做题:
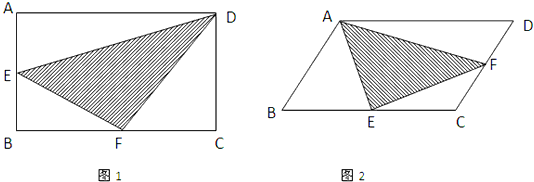
(1)如图1,已知阴影部分的面积是120平方厘米,E、F分别是长、宽的中点,长方形的宽是16厘米,求长方形的面积.
(2)如图2,平行四边形的面积是128平方厘米,E、F分别是两边的中点.求阴影部分面积.

(1)如图1,已知阴影部分的面积是120平方厘米,E、F分别是长、宽的中点,长方形的宽是16厘米,求长方形的面积.
(2)如图2,平行四边形的面积是128平方厘米,E、F分别是两边的中点.求阴影部分面积.

分析:(1)根据长方形的面积=长×宽=三角形BEF面积+三角形FC面积D+三角形AED面积+阴影部分面积,设出长方形的长,列方程解答出长的长度,再根据面积公式计算;
(2)由题意得:阴影部分面积=平行四边形的面积-三角形ABE面积-三角形ECF面积-三角形AFD面积,三角形ABE面积=BE×h÷2,三角形ECF面积=EC×
h÷2,三角形AFD面积=AD×
h÷2,所以三个三角形的面积和为:BE×h÷2+EC×
h÷2+AD×
h÷2=(
BE+
EC+
AD)h=
ADh=
×平行四边形的面积,再代数计算出阴影部分面积即可.
(2)由题意得:阴影部分面积=平行四边形的面积-三角形ABE面积-三角形ECF面积-三角形AFD面积,三角形ABE面积=BE×h÷2,三角形ECF面积=EC×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 8 |
| 5 |
| 8 |
解答:解:(1)设长方形的长是x厘米,由题意得:
16x=8x÷2+8×
x÷2+16×
x÷2+120,
16x=4x+2x+4x+120,
16x-10x=120,
6x=120,
x=20.
则长方形的面积为:16×20=320(平方厘米).
答:长方形的面积是320平方厘米.
(2)由题意得:阴影部分面积为:
128-
×128,
=128-80,
=48(平方厘米).
答:阴影部分面积是48平方厘米.
16x=8x÷2+8×
| 1 |
| 2 |
| 1 |
| 2 |
16x=4x+2x+4x+120,
16x-10x=120,
6x=120,
x=20.
则长方形的面积为:16×20=320(平方厘米).
答:长方形的面积是320平方厘米.
(2)由题意得:阴影部分面积为:
128-
| 5 |
| 8 |
=128-80,
=48(平方厘米).
答:阴影部分面积是48平方厘米.
点评:解决本题的关键是将所求图形的面积与已知面积相联系,利用等量关系解答.

练习册系列答案
相关题目
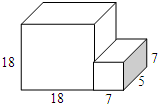 看图做题:
看图做题:
 、
、 、
、 、
、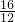 、________、________.
、________、________.
 ,相当于小平行四边形面积的
,相当于小平行四边形面积的 .大平行四边形与小平行四边形的面积比是________,如果大平行四边形的面积是60平方厘米,那么,小平行四边形的面积是________平方厘米.
.大平行四边形与小平行四边形的面积比是________,如果大平行四边形的面积是60平方厘米,那么,小平行四边形的面积是________平方厘米.