题目内容
在矩形ABCD中，E、F分别是AD、AB的中点，四边形AFCE的面积是18cm2，则矩形ABCD的面积是________cm2．
36
分析：连接AC．根据中线的性质，三角形面积与底的正比关系可得S△AFC=S△BFC，S△AEC=S△DEC，可得四边形AFCE的面积是矩形ABCD的面积的一半，从而求解．
解答：
解：连接AC．
因为E、F分别是AD、AB的中点，
所以S△AFC=S△BFC，S△AEC=S△DEC，
所以四边形AFCE的面积是矩形ABCD的面积的一半，
所以矩形ABCD的面积是：18×2=36cm2．
故答案为：36．
点评：考查了长方形的面积和三角形面积与底的正比关系，本题的关键是作出辅助线将四边形AFCE的面积与矩形ABCD的面积联系起来．
分析：连接AC．根据中线的性质，三角形面积与底的正比关系可得S△AFC=S△BFC，S△AEC=S△DEC，可得四边形AFCE的面积是矩形ABCD的面积的一半，从而求解．
解答：
解：连接AC．因为E、F分别是AD、AB的中点，
所以S△AFC=S△BFC，S△AEC=S△DEC，
所以四边形AFCE的面积是矩形ABCD的面积的一半，
所以矩形ABCD的面积是：18×2=36cm2．
故答案为：36．
点评：考查了长方形的面积和三角形面积与底的正比关系，本题的关键是作出辅助线将四边形AFCE的面积与矩形ABCD的面积联系起来．
练习册系列答案
相关题目
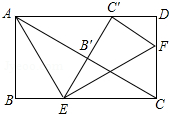如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为
如图，矩形ABCD的长、宽分别为