题目内容
 如图.△ABC是一个直角三角形,CD=CE,∠CDE=35度,∠BAC等于________度.
如图.△ABC是一个直角三角形,CD=CE,∠CDE=35度,∠BAC等于________度.
20
分析:观察图形可知,在直角三角形中,∠BAC+∠ACB=90度,所以只要求出∠ACB的度数即可解答:因为CD=CE,所以可以得出:∠CDE=∠CDE=35度;再根据三角形内角和定理可得∠ECD=180-35-35=110度,据此可以得出∠ACB=180-110=70度,据此即可解答.
解答:因为CD=CE,所以:∠CDE=∠CDE=35度;
则:∠ECD=180-35-35=110(度),
所以∠ACB=180-110=70(度),
则∠BAC=90-70=20(度),
答:∠BAC等于20度.
故答案为:20.
点评:此题主要考查三角形内角和定理的计算以及等腰三角形的性质的应用.
分析:观察图形可知,在直角三角形中,∠BAC+∠ACB=90度,所以只要求出∠ACB的度数即可解答:因为CD=CE,所以可以得出:∠CDE=∠CDE=35度;再根据三角形内角和定理可得∠ECD=180-35-35=110度,据此可以得出∠ACB=180-110=70度,据此即可解答.
解答:因为CD=CE,所以:∠CDE=∠CDE=35度;
则:∠ECD=180-35-35=110(度),
所以∠ACB=180-110=70(度),
则∠BAC=90-70=20(度),
答:∠BAC等于20度.
故答案为:20.
点评:此题主要考查三角形内角和定理的计算以及等腰三角形的性质的应用.

练习册系列答案
相关题目
 如图,ABC是一个直角等腰三角形,直角边的长度是1米.现在以C点为圆心,把三角形ABC顺时针旋转90度,那么,AB边在旋转时所扫过的面积是
如图,ABC是一个直角等腰三角形,直角边的长度是1米.现在以C点为圆心,把三角形ABC顺时针旋转90度,那么,AB边在旋转时所扫过的面积是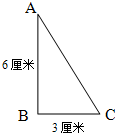 如图,ABC是直角三角形,以AB为轴并将三角形绕这个轴旋转一周得到一个旋转体,求这个旋转体的体积.
如图,ABC是直角三角形,以AB为轴并将三角形绕这个轴旋转一周得到一个旋转体,求这个旋转体的体积.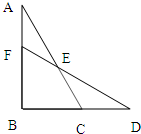 如图.△ABC是一个直角三角形,CD=CE,∠CDE=35度,∠BAC等于
如图.△ABC是一个直角三角形,CD=CE,∠CDE=35度,∠BAC等于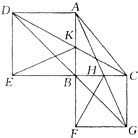 如图,ABC是一个直角三角形,AB≠CB,ABED和BCGF是正方形.AG、BC交于H,DC,AB交于K.那么在此图中,与三角形ABC面积相等的三角形(不包括三角形ABC)的个数是( )
如图,ABC是一个直角三角形,AB≠CB,ABED和BCGF是正方形.AG、BC交于H,DC,AB交于K.那么在此图中,与三角形ABC面积相等的三角形(不包括三角形ABC)的个数是( )