题目内容
 如图所示,AB是半圆的直径,O是圆心,弧AC=弧CD=弧DB,M是弧CD的中点,H是弦CD的中点,若N是OB上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是
如图所示,AB是半圆的直径,O是圆心,弧AC=弧CD=弧DB,M是弧CD的中点,H是弦CD的中点,若N是OB上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是2
2
平方厘米.分析:如图所示,连接OC、OD、OH,则扇形AOC、COD、DOB的面积相等,都等于半圆面积的
,又因三角形COH与三角形CNH等底等高,则二者的面积相等,所以阴影部分的面积等于扇形COD的一半,从而可以求出阴影部分的面积.
| 1 |
| 3 |
解答:解: 连接OC、OD、OH,则扇形AOC、COD、DOB的面积相等,都等于半圆面积的
连接OC、OD、OH,则扇形AOC、COD、DOB的面积相等,都等于半圆面积的
,
又因三角形COH与三角形CNH等底等高,则二者的面积相等,所以阴影部分的面积等于扇形COD的一半;
12×
×
,
=4×
,
=2(平方厘米);
答:图中阴影部分的面积是2平方厘米.
故答案为:2.
 连接OC、OD、OH,则扇形AOC、COD、DOB的面积相等,都等于半圆面积的
连接OC、OD、OH,则扇形AOC、COD、DOB的面积相等,都等于半圆面积的| 1 |
| 3 |
又因三角形COH与三角形CNH等底等高,则二者的面积相等,所以阴影部分的面积等于扇形COD的一半;
12×
| 1 |
| 3 |
| 1 |
| 2 |
=4×
| 1 |
| 2 |
=2(平方厘米);
答:图中阴影部分的面积是2平方厘米.
故答案为:2.
点评:解答此题的关键是:作出合适的辅助线,得到阴影部分与半圆的面积的关系,是解答本题的关键.

练习册系列答案
相关题目
 如图所示,AB是半圆的直径,O是圆心,AB=CD=DB,M是 CD 的中点,H是弦CD的中点,若N是OB上的一点,半圆面积等于12平方厘米,则图中阴影部分的面积是多少?
如图所示,AB是半圆的直径,O是圆心,AB=CD=DB,M是 CD 的中点,H是弦CD的中点,若N是OB上的一点,半圆面积等于12平方厘米,则图中阴影部分的面积是多少? 如图所示的半圆的直径BC=8cm,AB=AC,D是AC的中点,则阴影部分的面积是
如图所示的半圆的直径BC=8cm,AB=AC,D是AC的中点,则阴影部分的面积是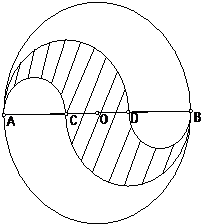 AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积.
AB是圆O的直径,其长为1,它的三等分点分别为C与D,在AB的两侧以AC、AD、CB、DB为直径分别画圆(如图所示).这四个半圆将原来的圆分成三部分,求其中阴影部分面积. 如图所示,AB是半圆的直径,O是圆心,AB=CD=DB,M是 CD 的中点,H是弦CD的中点,若N是OB上的一点,半圆面积等于12平方厘米,则图中阴影部分的面积是多少?
如图所示,AB是半圆的直径,O是圆心,AB=CD=DB,M是 CD 的中点,H是弦CD的中点,若N是OB上的一点,半圆面积等于12平方厘米,则图中阴影部分的面积是多少?