Question

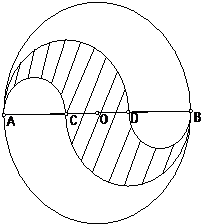AB是圆O的直径，其长为1，它的三等分点分别为C与D，在AB的两侧以AC、AD、CB、DB为直径分别画圆（如图所示）．这四个半圆将原来的圆分成三部分，求其中阴影部分面积．

Answer 1

分析：由图意可知：阴影部分的面积=以AD为直径的圆的面积-以AC为直径的面积，又因AB的长度已知，C、D是AB的三等分点，于是可以求出AC、AD的长度，进而利用圆的面积公式即可求解．

解答：解：因为AB=1，C、D是AB的三等分点，
所以AC=

1

3

，AD=

2

3

，
阴影部分的面积是：
π×[(

2

3

)2-(

1

3

)2]，
=π×（

4

9

-

1

9

），
=

1

3

π；
答：阴影部分的面积是

1

3

π．

点评：本题考查了面积与等积变换的应用，关键是能根据图形得出阴影部分的面积是以AD为直径的圆的面积减去以AC为直径的圆的面积，主要考查学生的计算能力和观察图形的能力．