题目内容
【题目】如图，凸四边形ABCD的边AD和BC的延长线相交于点E，H和G分别是BD和AC的中点．求：△EHG的面积与四边形ABCD的面积之比．
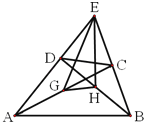
【答案】1：4．
【解析】
试题分析：要求S△EHG和四边形ABCD的比例关系，首先要将S△EHG和四边形ABCD分别与与之有关联的图形进行转换，通过观察发现：S△GHC=S△AGH，S△DGC=S△ADG，于是求得S△GHC+S△DGC之和即四边形DGHC的面积为四边形AHCD的一半．同理可求得四边形AHCD的面积为四边形ABCD的一半，于是得出四边形ABCD的面积为四边形GHCD的4倍．
然后求出S△GHE与S四边形GHCD的关系即可．
解：如图所示：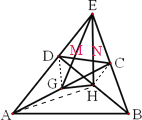
；
连接DG、HC、AH，设DC与GE交于M，DC与EH交于N，设△ENC=S1，S△EMN=S2，S△DME=S3，S△HNC=S4，S△DGM=S5．
因：S△EHB=S△DHE，故：S1+S4+S△BHC=S2+S3+S△DHN…1
又因：S△DHC=S△BHC，故：S△DHN+S4=S△BHC…2
将2代入1得出：S1+S4+S4+S△DHN=S2+S3+S△DHN 简化得出：2S4=S2+S3﹣S1…3
同理：S△AGE=S△EGC，故：S△GMC+S1+S2=S3+S5+S△ADG…4
S△ADG=S△DGC，故：S△GMC+S5=S△ADG…5
将5代入4，得出：S△GMC+S1+S2=S3+S5+S△GMC+S5，简化得出：2S5=S1+S2﹣S3…6
将得式3与得式6相加，得出：S4+S5=S2，故：S△GHE=S四边形GHCD…7
又因：S△GHC=S△AGH，S△DGC=S△ADG，故：S四边形DGHC的=1/2 S四边形AHCD，同理可求得S四边形AHCD=
S四边形ABCD，于是得出：S四边形ABCD=4 S四边形GHCD…8
故 S△EHG：S四边形ABCD=1：4
答：△EHG的面积与四边形ABCD的面积之比是1：4．
