题目内容
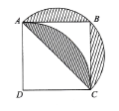
【题目】正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积。
【答案】1.14平方厘米
【解析】根据图示可知，阴影部分的面积等于正方形外阴影部分的面积加上正方形内阴影部分的面积，扇形ABC是以AC为直径的圆的面积的一半，可用以AC为直径的圆的面积的一半减去正方形面积的一半就是正方形外阴影部分的面积，正方形内阴影部分的面积等于以AD为半径的
圆的面积减去三角形ACD的面积，列式解答即可得到答案。
解：AC的长为2厘米，半径为1厘米。
正方形外阴影部分的面积为：3.14×12×
-2×1÷2
=3.14×-1
=1.57-1
=0.57（平方厘米）
正方形内阴影部分的面积为：3.14×2×-2÷2
=6.28×-1
=1.57-1
=0.57（平方厘米）
0.57+0.57=1.14（平方厘米）
答：阴影部分的面积为1.14平方厘米。
练习册系列答案
阅读快车系列答案
相关题目