题目内容
4.-些图片按下面的方式摆放.请填写下表.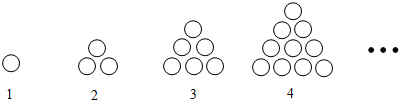
| 堆数 | 圆片数与堆数的关系 | 圆片数/个 |
| 第1堆 | ||
| 第2堆 | ||
| 第3堆 | ||
| 第4堆 | ||
| 第n堆 |
分析 第一堆1个○,1=$\frac{1×(1+1)}{2}$、第二堆3个○,3=$\frac{2×(2+1)}{2}$、第三堆6个○,6=$\frac{3×(3+1)}{2}$、第四堆10个○,10=$\frac{4×(4+1)}{2}$…每堆○片的个数=$\frac{堆序号×(堆序号+1)}{2}$,即第n堆○的个数是$\frac{n(n+1)}{2}$.
解答 解:些图片按下面的方式摆放.请填写下表如下:
| 堆数 | 圆片数与堆数的关系 | 圆片数/个 |
| 第1堆 | ○片的个数=1=$\frac{1×(1+1)}{2}$ | 1 |
| 第2堆 | ○片的个数=3=$\frac{2×(2+1)}{2}$ | 3 |
| 第3堆 | ○片的个数=6=$\frac{3×(3+1)}{2}$ | 6 |
| 第4堆 | ○片的个数=10=$\frac{4×(4+1)}{2}$ | 10 |
| 第n堆 | ○片的个数=$\frac{n(n+1)}{2}$ | $\frac{n(n+1)}{2}$ |
点评 此题称杨辉三角,又称贾宪三角形,帕斯卡三角形.帕斯卡是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年.关键是找规律,再根据规律求圆片的个数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.直接写出得数
| 130×5= | 2×380= | 300×60= | 620+30= |
| 26×20= | 250×20= | 156-99= | 200×40= |
| 50×90= | 300×40= | 16×400= | 21×40= |
 看图填空:
看图填空: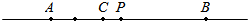 如图,相距5km的A、B两地间有一条笔直的马路.C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回.到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问:
如图,相距5km的A、B两地间有一条笔直的马路.C地位于AB两地之间且距A地2km,小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动,当到达B地后立即以原来的速度返回.到达A地停止运动,设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点,以从A到B为正方向,用1个单位长度表示1km,解答下列各问: