题目内容
(1)大于
而小于
的分数只有
.
(2 ) 把153分解质因数是153=3×51.
(3)甲数比乙数多20%,乙数就比甲数少
.
(4)圆锥的体积都小于圆柱的体积.
(5)把13米长的绳子平均分成26段,每段占原长的
.
| 1 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
错误
错误
(2 ) 把153分解质因数是153=3×51.
错误
错误
(3)甲数比乙数多20%,乙数就比甲数少
| 1 |
| 5 |
错误
错误
(4)圆锥的体积都小于圆柱的体积.
错误
错误
(5)把13米长的绳子平均分成26段,每段占原长的
| 1 |
| 2 |
错误
错误
.分析:(1)大于
而小于
的同分母的分数,只有一个
,而不同分母的分数有很多个,如
、
等.据此解答即可.
(2)分解质因数就是把一个合数写成几个质数的连乘积形式,一般先从简单的质数试着分解.
(3)由甲数比乙数多20%,把乙数看做单位“1”,甲数对应的分率就是(1+20%),要求乙数比甲数少几分之几,就是求乙数比甲数少的部分是甲数的几分之几,列式计算后再判断.
(4)根据圆柱的体积公式,V=sh,及圆锥的体积公式,V=
sh,知道圆柱的体积与圆锥的体积都与底面积和高有关,由于圆柱的底面积与高及圆锥的底面积与高都不确定,所以不能判断圆柱的体积比圆锥的体积大.
(5)把绳子的总米数看做单位“1”,求每段占绳子全长的几分之几,平均分的是单位“1”的量,就用1除以26即可.据此计算并判断.
| 1 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
| 14 |
| 6 |
| 14 |
(2)分解质因数就是把一个合数写成几个质数的连乘积形式,一般先从简单的质数试着分解.
(3)由甲数比乙数多20%,把乙数看做单位“1”,甲数对应的分率就是(1+20%),要求乙数比甲数少几分之几,就是求乙数比甲数少的部分是甲数的几分之几,列式计算后再判断.
(4)根据圆柱的体积公式,V=sh,及圆锥的体积公式,V=
| 1 |
| 3 |
(5)把绳子的总米数看做单位“1”,求每段占绳子全长的几分之几,平均分的是单位“1”的量,就用1除以26即可.据此计算并判断.
解答:解:(1)大于
而小于
的同分母的分数,只有一个
,而不同分母的分数有很多个,如
、
等,
故答案为:错误.
(2)
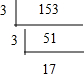
把153分解质因数为:153=3×3×17.
故答案为:错误.
(3)甲数对应的分率:1+20%=
,
乙数比甲数少:(
-1)÷
=
×
=
;
故答案为:错误.
(4)因为,圆柱的体积公式,V=sh,圆锥的体积公式,V=
sh,
所以,圆柱的体积与圆锥的体积都与底面积和高有关;
由于圆柱的底面积与高及圆锥的底面积与高都不确定,
所以不能判断圆柱的体积比圆锥的体积大;
故答案为:错误.
(5)每段占绳子全长的:1÷26=
.
故答案为:错误.
| 1 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
| 14 |
| 6 |
| 14 |
故答案为:错误.
(2)

把153分解质因数为:153=3×3×17.
故答案为:错误.
(3)甲数对应的分率:1+20%=
| 6 |
| 5 |
乙数比甲数少:(
| 6 |
| 5 |
| 6 |
| 5 |
| 1 |
| 5 |
| 5 |
| 6 |
| 1 |
| 6 |
故答案为:错误.
(4)因为,圆柱的体积公式,V=sh,圆锥的体积公式,V=
| 1 |
| 3 |
所以,圆柱的体积与圆锥的体积都与底面积和高有关;
由于圆柱的底面积与高及圆锥的底面积与高都不确定,
所以不能判断圆柱的体积比圆锥的体积大;
故答案为:错误.
(5)每段占绳子全长的:1÷26=
| 1 |
| 26 |
故答案为:错误.
点评:(1)本题的关键是引导学生走出:大于
而小于
的同分母的分数,只有一个
的误区,还有很多异分母的分数.
(2)此题主要考查了把一个合数分解质因数的方法.
(3)此题考查根据一个数比另一个数多(或少)百分之几,求另一个数比一个数少(或多)几分之几,两句话中单位“1”的量不同,分率就肯定不同;也可以通过计算而得解.
(4)此题主要考查了圆柱与圆锥的体积公式的实际应用,即必须是在等底等高的条件下圆锥的体积比圆柱的体积小.
(5)此题考查把单位“1”平均分成若干份,取其中的一份,就用几分之一来表示.
| 1 |
| 7 |
| 3 |
| 7 |
| 2 |
| 7 |
(2)此题主要考查了把一个合数分解质因数的方法.
(3)此题考查根据一个数比另一个数多(或少)百分之几,求另一个数比一个数少(或多)几分之几,两句话中单位“1”的量不同,分率就肯定不同;也可以通过计算而得解.
(4)此题主要考查了圆柱与圆锥的体积公式的实际应用,即必须是在等底等高的条件下圆锥的体积比圆柱的体积小.
(5)此题考查把单位“1”平均分成若干份,取其中的一份,就用几分之一来表示.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目