Question

18．一个圆的外切正方形的面积是它的内接正方形的2倍．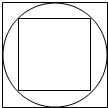

Answer 1

分析 设圆的半径为r，则内接正方形的边长为$\sqrt{2}$r，其面积是（$\sqrt{2}$r）²=2r²，外切圆的边长为2r，其面积为（2r）²=4r²，用外切正方形面积除以内接正方形面积．

解答 解：设圆的半径为r．
则内接正方形的边长为$\sqrt{2}$r，
其面积是（$\sqrt{2}$r）²=2r²，
外切圆的边长为2r，
其面积为（2r）²=4r²，
4r²÷2r²=2．
答：一个圆的外切正方形的面积是它的内接正方形的2倍．
故答案为：2．

点评 此题单独求两个正方形的面积不好求，这两个正方形都与这个圆有关系，巧妙地利用这两个正方形边长与圆半径的关系，求出含有这个圆半径的两个正方形的面积，从而使问题得到解决．