题目内容
20．
如图，正方形ABCD的边长是4cm，DE长4.5cm．AF垂直DE于F，则AF=$\frac{32}{9}$厘米．
分析 如图，连接AE，求三角形ADE的面积，三角形ADE的面积：4×4÷2=8（平方厘米），在三角形ADE中，已经知道面积和底了，就可以求高了，即AF，用面积乘以2除以底，即可求出高的值，计算即可．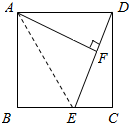
解答 解：如上图，连接AE，
S△ADE=4×4÷2=8（平方厘米），
又因为S△ADE=DE×AF÷2，DE=4.5，
所以AF=8×2÷4.5
=16÷4.5
=$\frac{32}{9}$（厘米）
答：AF等于$\frac{32}{9}$厘米．
故答案为：$\frac{32}{9}$．
点评 此题重点考查了三角形的面积与底的关系，在此题中，求出S△ADE的面积是解决此题的关键．
练习册系列答案
相关题目