题目内容
16.有一个长方体,它的正面和上面的面积之和是77,如果这个长方体的长、宽、高都是质数,要从这个长方体上割下尽可能大的正方体,最多有几个?分析 根据题意:一个长方体前面和上面的面积=长×高+长×宽=长×(高+宽)=77,又知它的长、宽、高都是整厘米,且都是质数,77只有1种组合11×7,11不可再分,因为11=2+9=3+8=4+7=1+10=5+6,都不符合条件,7只能分为2、5,所以割下尽可能大的正方体,最大为棱长为2厘米,共(11÷2)×(5÷2)×(2÷2)=10个;由此解答即可.
解答 解:一个长方体前面和上面的面积=长×高+长×宽=长×(高+宽)=77,
77=11×7=11×(2+5),
所以,长宽高分别为2、5、11,
割下尽可能大的正方体,最大为棱长为2,共
(11÷2)×(5÷2)×(2÷2)
≈5×2×1
=10(个)
答:要从这个长方体上割下尽可能大的正方体,最多有10个.
点评 解此题关键是熟记长方体的表面积和体积公式,再根据题意确定长、宽、高是多少.

练习册系列答案
相关题目

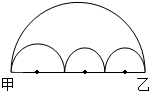 如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同)
如图,两只蚂蚁同时从甲地爬向乙地,一只蚂蚁沿着大半圆爬行,哪只蚂蚁先到达乙地?为什么?(两只蚂蚁的爬行速度相同)