题目内容
 -2.03=3.02 -2.03=3.02 | 5×6x-3x=1 |  ×(x- ×(x- )= )= | 6 x-2 x-2 × × =4× =4× |
| 72×3-7x=0.06 | x:1 =1 =1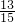 :1 :1 | 12×(47+x)=1152 |  x+ x+ x=42. x=42. |
解:(1) -2.03=3.02,
-2.03=3.02,
 -2.03+2.03=3.02+2.03,
-2.03+2.03=3.02+2.03,
 =5.05,
=5.05,
 ×20=5.05×20,
×20=5.05×20,
x=101;
(2)5×6x-3x=1,
27x=1,
27x÷27=1÷27,
x= ;
;
(3) ×(x-
×(x- )=
)= ,
,
 ×(x-
×(x- )×
)× =
= ×
× ,
,
x- =1,
=1,
x- +
+ =1+
=1+ ,
,
x=1 ;
;
(4)6 x-2
x-2 ×
× =4×
=4× ,
,
6 x-
x- =2,
=2,
6 x-
x- +
+ =2+
=2+ ,
,
6 x=
x= ,
,
6 x×
x×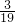 =
= ×
×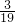 ,
,
x=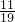 ;
;
(5)72×3-7x=0.06,
216-7x=0.06,
216-7x+7x=0.06+7x,
0.06+7x=216,
0.06+7x-0.06=216-0.06,
7x÷7=215.094÷7,
x≈30.84;
(6)x:1 =1
=1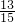 :1
:1 ,
,
1 x=
x= ×
×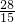 ,
,
1 x×
x× =
= ×
×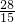 ×
× ,
,
x=2;
(7)12×(47+x)=1152,
12×(47+x)÷12=1152÷12,
47+x=96,
47+x-47=96-47,
x=49;
(8) x+
x+ x=42,
x=42,
 x=42,
x=42,
 x×
x× =42×
=42× ,
,
x=36.
分析:(1)根据等式的性质,方程两边同时加上2.03,再同时乘20求解;
(2)先化简得27x=1,再根据等式的性质,方程两边同时除以27求解;
(3)根据等式的性质,方程两边同时 ,再同时加上
,再同时加上 求解;
求解;
(4)先化简得6 x-
x- =2,再根据等式的性质,方程两边同时加上
=2,再根据等式的性质,方程两边同时加上 ,再同时乘
,再同时乘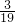 求解;
求解;
(5)先化简得216-7x=0.06,再根据等式的性质,方程两边同时加上7x,再同时减去0.06,最后同时除以7求解;
(6)根据比例的基本性质,方程变为 1 x=
x= ×
×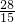 ,再根据等式的性质,两边同时乘
,再根据等式的性质,两边同时乘 即可;
即可;
(7)根据等式的性质,方程两边同时除以12,再同时减去47求解;
(8)先化简得 x=42,再根据等式的性质,方程两边同时乘
x=42,再根据等式的性质,方程两边同时乘 求解;
求解;
点评:此题考查了学生解方程的能力,解方程一定要注意格式,遵循等式性质.
 -2.03=3.02,
-2.03=3.02, -2.03+2.03=3.02+2.03,
-2.03+2.03=3.02+2.03, =5.05,
=5.05, ×20=5.05×20,
×20=5.05×20,x=101;
(2)5×6x-3x=1,
27x=1,
27x÷27=1÷27,
x=
 ;
;(3)
 ×(x-
×(x- )=
)= ,
, ×(x-
×(x- )×
)× =
= ×
× ,
,x-
 =1,
=1,x-
 +
+ =1+
=1+ ,
,x=1
 ;
;(4)6
 x-2
x-2 ×
× =4×
=4× ,
,6
 x-
x- =2,
=2,6
 x-
x- +
+ =2+
=2+ ,
,6
 x=
x= ,
,6
 x×
x×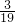 =
= ×
×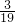 ,
,x=
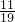 ;
;(5)72×3-7x=0.06,
216-7x=0.06,
216-7x+7x=0.06+7x,
0.06+7x=216,
0.06+7x-0.06=216-0.06,
7x÷7=215.094÷7,
x≈30.84;
(6)x:1
 =1
=1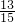 :1
:1 ,
,1
 x=
x= ×
×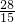 ,
,1
 x×
x× =
= ×
×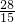 ×
× ,
,x=2;
(7)12×(47+x)=1152,
12×(47+x)÷12=1152÷12,
47+x=96,
47+x-47=96-47,
x=49;
(8)
 x+
x+ x=42,
x=42, x=42,
x=42, x×
x× =42×
=42× ,
,x=36.
分析:(1)根据等式的性质,方程两边同时加上2.03,再同时乘20求解;
(2)先化简得27x=1,再根据等式的性质,方程两边同时除以27求解;
(3)根据等式的性质,方程两边同时
 ,再同时加上
,再同时加上 求解;
求解;(4)先化简得6
 x-
x- =2,再根据等式的性质,方程两边同时加上
=2,再根据等式的性质,方程两边同时加上 ,再同时乘
,再同时乘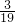 求解;
求解;(5)先化简得216-7x=0.06,再根据等式的性质,方程两边同时加上7x,再同时减去0.06,最后同时除以7求解;
(6)根据比例的基本性质,方程变为 1
 x=
x= ×
×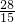 ,再根据等式的性质,两边同时乘
,再根据等式的性质,两边同时乘 即可;
即可;(7)根据等式的性质,方程两边同时除以12,再同时减去47求解;
(8)先化简得
 x=42,再根据等式的性质,方程两边同时乘
x=42,再根据等式的性质,方程两边同时乘 求解;
求解;点评:此题考查了学生解方程的能力,解方程一定要注意格式,遵循等式性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目